Differences between revisions 15 and 20 (spanning 5 versions)

Statistical Tests for Experiments with Single Samples

Sometimes, the research question is as simple as investigating whether the value of a certain property of a group differs from a hypothetical value (specified by the null hypothesis). Depending on what information is available, one can choose between the following types of tests:

In this section, we are going to review these tests by working through a few toy problems.

Z-test

The z-test is often used to compare a set of experimental measurements to a given constant as specified by the null hypothesis. For example, suppose that we know the mean and standard deviation of neuronal density of the frontal cortex, our research interest is to investigate whether Einstein's neuronal density is significantly different from the average -- the test statistic under the null hypothesis. The z-test is appropriate in such contexts.

Note that conducting a z-test requires that information other than the variable of interest is available. For instance, the standard deviation of the neuronal density in the target population (not the sample!) must be known -- or at least can be estimated with reasonably high accuracy (i.e. if the sample size of your experiment is on the order of thousands). If, however, the sample size of your experiment is small and no information regarding the standard deviation of the population is available, the t-test is recommended.

Example Problem

In order to test the effectiveness of a human growth drug, you administer the drug to 16 boys, aged 14. Six years later, you measure their heights and find an average height for your subjects of 71 inches. You know that the average height of American males is 70 inches and the standard deviation is 9 inches.

The first step is always to identify the null hypothesis. In this case, the null hypothesis can be:

$H_{0}$ : Teenage boys who take the human growth drug will not grow faster or slower than average American males.

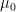In mathematical terms, the null hypothesis is that $\mu=\mu_{0}$ , where $\mu$ stands for the population mean of teenage boys who take the human growth drug, and $\mu_{0}$ the population mean of American males.

We will assume that the $\alpha$ level is set to 0.05 and the test is two-tailed.

Solve the Problem by Hand

To determine whether or not we should reject the null hypothesis, we need to calculate the z statistic 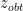$z_{obt}$ and then determine its significance. The formula for calculating 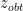$z_{obt}$ is:

$z_{obt} = \frac{\overline{X}_{obt} - \mu_{0}}{\sigma / \sqrt{N}}$

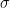where $\overline{X}_{obt}$ is the sample mean, $\mu_0$ the population mean of American males, $\sigma$ the population standard deviation, and N the sample size. Plugging in the numbers, it is easy to get:

$z_{obt} = \frac{71 - 70}{9 / \sqrt{16}} = 0.444$

Finally, we need to determine whether the effect is significant based on the calculated 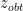$z_{obt}$ . One can look up in the z table (usually the first Appendix table in a stats textbook) and find out the critical value for $\alpha = 0.05$ and a two-tailed test is 1.96. The critical z score is clearly larger than the calculated 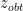$z_{obt}$ ; therefore, we retain the null hypothesis.

Conclusion: from the current experiment, there is not enough evidence to show that the growth drug is effective. (Be careful not to conclude that the null hypothesis is TRUE. Failure to reject to the null hypothesis does not mean the null hypothesis is correct.)

Single-sample t-test

The single-sample t-test is often more commonly used as we as experimenters rarely know the true standard deviation of the target population. The only available information has to come from the sample data collected in the experiment. For example, Smokin' Joe wants to know whether marijuana can increase appetite and conducted an experiment:

Example Problem

Smokin’ Joe hypothesizes that marijuana can be used to mitigate some of the negative side effects of common AIDS drugs, such as loss of appetite. He wants to test the hypothesis that marijuana increases the appetites of AIDS patients who are taking common AIDS drugs. He measures the difference in calories eaten by patients the day after taking a THC pill and the day before taking the pill. Here are the measurements he obtains for 10 subjects – [101, 75, -82, 32, -50, 203, 165, 145, 303, 23]

In other words, Smokin' Joe wants to test whether the difference in calories eaten by AIDS patients (i.e. the property of a group) is different from 0 (i.e. a hypothetical value). If it is significantly different from 0, we can reject the null hypothesis which states that marijuana has no effect on appetite.

Note here the only information available is the difference scores of the 10 subjects. We do not know the true standard deviation of the population of difference scores. Therefore, a z-test is not applicable in this case.

Approximate Population SD with Sample SD

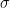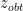One possible solution to the problem, which allows us to use the single-sample t-test, is to approximate the population standard deviation $\sigma$ with sample standard deviation $s$ . Recall that the equation to calculate the z statistic $z_{obt}$ is:

$z_{obt} = \frac{\overline{X}_{obt} - \mu}{\sigma / \sqrt{N}}$

In the single sample 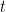$t$ test, we simply replace 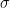$\sigma$ with the standard deviation of the sample $s$ to get 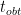$t_{obt}$ :

$t_{obt} = \frac{\overline{X}_{obt} - \mu}{s / \sqrt{N}}$

Once we have calculated 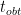$t_{obt}$ , we need to determine the significance of the statistic. If you are working with a stats program, the significance 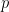$p$ value, including the 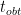$t_{obt}$ , is calculated automatically for you. If you are working with pen and paper, you will need to look up in the t distribution table (usually in the appendix of any statistics textbook) for the corresponding $t_{crit}$ value. In looking for the correct critical value to compare with, we also need to determine the degrees of freedom (DF) of the current test. 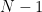For any single-sample t test, the DF is $N-1$ , where N is the sample size. It is then easy to locate the critical value in the table by choosing the right test (one-tailed or two-tailed?), the $\alpha$ level, and the DF.

Solve the Example Problem By Hand

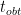Now we proceed to solve the example problem. Let's do a two-tailed test (see GeneralGuidance for topics on how to choose between a two-tailed test and a one-tailed test) with $\alpha$ value set to 0.05. To calculate the $t_{obt}$ , we calculate the following items first:

The sample average difference score $\overline{X}_{obt} = 91.5$
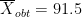
The population average difference score 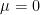$\mu = 0$ (by definition; since we want to know whether there is a change)
The sample standard deviation

Note: always carry at least three decimal places if working by hand. Rounding excessively in intermediate steps can lead to very very very inaccurate results.

Now we plug these numbers in the above equation:

$t_{obt} = \frac{\overline{X}_{obt} - \mu}{s / \sqrt{N}} = \frac{91.5-0}{117.449 / 3.162} = 2.463$

Looking up in the critical values table for the t distribution, we find that $t_{crit} = 2.262$ given that DF is 9 and $\alpha$ is 0.05 for a two-tailed test. Since our t statistic is greater than the critical value, we reject the null hypothesis. We conclude that Smokin' Joe's experimental results do not support the hypothesis that marijuana does not increase appetite.

It is extremely important to keep in mind that we cannot conclude that the experimental results support the alternative hypothesis, which states marijuana does increase appetite. The rejection of the null hypothesis, in frequentist statistics (which t-test belongs to), does not mean that the alternative hypothesis is TRUE.

-  ⇤ ← Revision 15 as of 2011-09-05 14:23:36 → 
  Size: 7225
  Editor: cpe-69-207-82-159
  Comment:
+   ← Revision 20 as of 2011-09-19 13:58:58 → ⇥
  Size: 8934
  Editor: colossus
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 5:
+  * [[#z-test-example|example problem]]
  * [[#z-test-solution|solve the problem by hand]]
-Line 11:
+Line 13:
- * [[#sign-test|sign test: when the experimental results are binary outcomes]]
  . In this section, we are going to review these tests by working through a few toy problems.
+In this section, we are going to review these tests by working through a few toy problems.
-Line 21:
+Line 22:
+<<Anchor(z-test-example)>>
-Line 26:
+Line 29:
-What is the null hypothesis?
+The first step is always to identify the null hypothesis. In this case, the null hypothesis can be:
-Line 29:
+Line 32:
+In mathematical terms, the null hypothesis is that <<latex($\mu=\mu_{0}$)>>, where <<latex($\mu$)>> stands for the population mean of teenage boys who take the human growth drug, and <<latex($\mu_{0}$)>> the population mean of American males.

We will assume that the <<latex($\alpha$)>> level is set to 0.05 and the test is two-tailed.

<<Anchor(z-test-solution)>>

=== Solve the Problem by Hand ===

To determine whether or not we should reject the null hypothesis, we need to calculate the z statistic <<latex($z_{obt}$)>> and then determine its significance. The formula for calculating <<latex($z_{obt}$)>> is:

{{{#!latex
\[
z_{obt} = \frac{\overline{X}_{obt} - \mu_{0}}{\sigma / \sqrt{N}}
\]
}}}

where <<latex($\overline{X}_{obt}$)>> is the sample mean, <<latex($\mu_0$)>> the population mean of American males, <<latex($\sigma$)>> the population standard deviation, and N the sample size. Plugging in the numbers, it is easy to get:

{{{#!latex
\[
z_{obt} = \frac{71 - 70}{9 / \sqrt{16}} = 0.444
\]
}}}

Finally, we need to determine whether the effect is significant based on the calculated <<latex($z_{obt}$)>>. One can look up in the z table (usually the first Appendix table in a stats textbook) and find out the critical value for <<latex($\alpha = 0.05$)>> and a two-tailed test is 1.96. The critical z score is clearly larger than the calculated <<latex($z_{obt}$)>>; therefore, we retain the null hypothesis.

'''Conclusion''': from the current experiment, there is not enough evidence to show that the growth drug is effective. (Be careful not to conclude that the null hypothesis is TRUE. Failure to reject to the null hypothesis does not mean the null hypothesis is correct.)
-Line 85:
+Line 116:
-It is extremely important to keep in mind that '''we cannot conclude that the experiments results support the alternative hypothesis, which states marijuana does increase appetite'''. The rejection of the null hypothesis, in frequentist statistics (which t-test belongs to), does not mean that the alternative hypothesis is TRUE.

<<Anchor(sign-test)>>

== Sign test (using binomial distribution) ==
The sign test is based on the binomial distribution
+It is extremely important to keep in mind that '''we cannot conclude that the experimental results support the alternative hypothesis, which states marijuana does increase appetite'''. The rejection of the null hypothesis, in frequentist statistics (which t-test belongs to), does not mean that the alternative hypothesis is TRUE.