|
Size: 7221
Comment:
|
Size: 7774
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 19: | Line 19: |
| == Unpaired/Independent Group t-test == | == Unpaired (independent) group t-test == |
| Line 24: | Line 24: |
| A physiologist has conducted an experiment to evaluate the effect of hormone X on sexual behavior. Ten rats were injected with hormone X and ten other rats received a placebo injection. The number of matings for each rate was counted over a 20 minute period. The test group had a sample mean number of matings = 8.4 and a sample std. deviation = 6.197. The place group had a sample mean number of matings = 5.6 and a sample std. deviation= 5.139. | A physiologist has conducted an experiment to evaluate the effect of hormone X on male sexual behavior. Ten rats were injected with hormone X and ten other rats received a placebo injection. Each rat was then housed with a female rat for 20 minutes, and the number of times each male mounted the female was counted. The test group had a sample mean number of mounts = 8.4 and a sample std. deviation = 6.197. The placebo group had a sample mean number of mounts = 5.6 and a sample std. deviation= 5.139. |
| Line 27: | Line 27: |
| Let's first identify the null hypothesis: The hormone has no effect on the number of times rats mate over a 20 minute period. Note that we have 20 rats here divided into two groups. Such a design is an independent group design and an unpaired t-test is appropriate. | Let's first identify the null hypothesis: The hormone has no effect on the number of times male rats mount a female during a 20 minute period. Note that we have 20 rats here divided into two groups. Such a design is an independent group design and an unpaired t-test is appropriate. |
| Line 31: | Line 31: |
| Now we test for a significant change in the mating rate of rats under the treatment of the hormone using an <<latex($\alpha = .05$)>> significance level. | Now we test for a significant change in the mating rate of rats under the treatment of the hormone using an <<latex($\alpha$)>> = 0.05 significance level. |
| Line 33: | Line 33: |
| We define <<latex($\mu_{null}$)>> as the mean of the null population. From the question, we know | We define ''D,,0,,'' as the difference in population means between the two conditions. The '''null hypothesis''' states that this value is 0: |
| Line 35: | Line 35: |
| {{{#!latex \[ mu_{null} = 0 \] }}} In other words, the null hypothesis states that the hormone has no effect. |
. ''H,,0,,'': The hormone has no effect on the mating rate of rats (''D,,0,,'' = 0). |
| Line 47: | Line 41: |
| x_{hormone} - x_{placebo} = 8.4-5.6=2.8 | \bar{D} = \bar{x}_{hormone} - \bar{x}_{placebo} = 8.4-5.6=2.8 |
| Line 51: | Line 45: |
| and the standard error of the difference in means (please compare this with '''the standard error of the mean difference''' in the paired t-test) | and the standard error of the difference in means can be computed from the variance of each sample <<latex($s^{2}_{hormone}$)>> and <<latex($s^{2}_{placebo}$)>>: |
| Line 55: | Line 49: |
| s_{x_{hormone} - x_{placebo}} = \sqrt{\frac{s^{2}_{hormone} + s^{2}_{placebo}}{N}} = \sqrt{\frac{6.197^{2} + 5.139^{2}}{10}} = 2.546 | se_{D} = \sqrt{\frac{s^{2}_{hormone} + s^{2}_{placebo}}{N}} = \sqrt{\frac{6.197^{2} + 5.139^{2}}{10}} = 2.546 |
| Line 59: | Line 53: |
| Finally, we can calculate our <<latex($t_{obt}$)>>, the formula is as follows: | Finally, we calculate the ''t,,obt,,''. The formula is as follows: |
| Line 63: | Line 57: |
| t_{obt} = \frac{x_{hormone}-x_{placebo}-\mu_{null}}{se} = \frac{2.8 - 0}{2.546} = 1.10 | t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.8 - 0}{2.546} = 1.10 |
| Line 67: | Line 61: |
| By looking up in the t distribution table, we find the 2-tailed t-critical value at DF = 2N − 2 = 18 is 2.101. Since our obtained t statistic is smaller than the critical value, we fail to reject the null hypothesis. There is no sufficient evidence to conclude that hormone X has an effect on the number of times rats mate over a 20-minute period. | By looking up in the t distribution table, we find the 2-tailed t-critical value at ''df = 2N − 2 = 18'' is ''2.101''. Since our obtained ''t''-statistic is smaller than the critical value, we fail to reject the null hypothesis. The data do not support the hypothesis that hormone X has an effect on the frequency of male rat mounting behavior during a 20-minute period. |
| Line 73: | Line 67: |
| == Paired/Repeated Group t-test == | == Paired (repeated-measures) t-test == |
| Line 82: | Line 76: |
| || Subject No. || Birth Control pill || Placebo pill || || 1 || 108 || 102 || || 2 || 76 || 68 || || 3 || 69 || 66 || || 4 || 78 || 71 || || 5 || 74 || 76 || || 6 || 85 || 80 || || 7 || 79 || 82 || || 8 || 78 || 79 || || 9 || 80 || 78 || || 10 || 81 || 85 || |
|| Subject No. || Placebo pill || Birth Control pill || || 1 || 102 || 108 || || 2 || 76 || 76 || || 3 || 66 || 69 || || 4 || 71 || 78 || || 5 || 68 || 74 || || 6 || 85 || 85 || || 7 || 82 || 79 || || 8 || 78 || 78 || || 9 || 79 || 80 || || 10 || 80 || 81 || |
| Line 94: | Line 88: |
| The first step, again, is to identify the null hypothesis: Birth control will not affect the blood pressure of women who are taking it (<<latex($\mu_{D} = 0$)>>). This also justifies a two-tailed test since we are not interested in whether the effect is directional (i.e. whether the birth control pill will increase or decrease blood pressure). | The first step, again, is to identify the null hypothesis: The birth control pill does not affect the blood pressure of women who are taking it (i.e. <<latex($D_0 = 0$)>>). A two-tailed test should be used since an effect in either direction (i.e. whether the birth control pill increases or decreases blood pressure) would be of interest. |
| Line 98: | Line 92: |
| Now we test for a significant change in the blood pressure of women on birth control pills using an <<latex($\alpha = .05$)>> significance level. | Now we test for a significant change in the blood pressure of women on birth control pills using an <<latex($\alpha$)>> = 0.05 significance level. |
| Line 104: | Line 98: |
| x_{obt} = 2.1 | \bar{D} = 2.1 |
| Line 110: | Line 104: |
| {{{#!latex \[ s = 4.383 \] }}} |
''s = 3.281'' |
| Line 116: | Line 106: |
| Now, the standard error of the mean: | Now, the standard error of the mean ''s,,D,,''>> is: |
| Line 121: | Line 111: |
| s_{\overline{x}} = \frac{s}{\sqrt{n}} = \frac{4.383}{\sqrt{10}} = 1.386 | se_{D} = \frac{s}{\sqrt{n}} = \frac{3.281}{\sqrt{10}} = 1.038 |
| Line 127: | Line 117: |
| And, finally, our <<latex($t_{obt}$)>>: | And, finally, our ''t,,obt,,'': |
| Line 131: | Line 121: |
| t_{obt} = \frac{x_{obt}-\mu_{D}}{s_{x}} = \frac{2.1 -0 }{1.386} = 1.515 | t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.1 -0 }{1.038} = 2.024 |
| Line 135: | Line 125: |
| '''What is the degrees of freedom for a paired t-test?''' Since we only have 10 subjects in our group, the DF is the same as in the one-sample t-test: N-1. Now, we can look up the critical value of t for a two-tail test using the alpha value 0.05 and the appropriate degrees of freedom (df = 10-1 = 9). The critical value is 2.262, which is larger than our obtained t statistic. Thus, we retain the null hypothesis and conclude that there is no sufficient evidence for the claim that the birth control pill affects the blood pressure of women who take it. | '''What is the degrees of freedom for a paired t-test?''' Since we only have 10 subjects in our group, the ''df'' is the same as in the one-sample t-test: ''N'' - 1. Now, we can look up the critical value of ''t'' for a two-tail test using the alpha value 0.05 and the appropriate degrees of freedom (''df'' = 10-1 = 9). The critical value is 2.262, which is larger than our obtained ''t''-statistic. Thus, we retain the null hypothesis and conclude that there is no sufficient evidence for the claim that the birth control pill affects the blood pressure of women who take it. '''Note:''' If you used a statistics program to calculate the result of the t-test, you will find the ''p''-value of this test is 0.074. When the ''p''-value is greater than 0.05 and less than 0.1, we often refer to the result as "marginally significant". A marginally significant result often indicates a weak but probable effect, and thus is worth mentioning. Reporting a result as "marginally significant" is a common practice in experimental sciences. |
Statistical Tests for Experiments with Two Samples
A common experimental design is taking measurements from both a test group and a control group. For example, we may want to test the effectiveness of a new drug. A scientifically reasonable way of conducting an experiment is to give the drug to the test group while giving the placebo to the control group. If there is a significant difference between the test group and the control group, we can conclude the drug is at least statistically improving patients' well-being.
An important concept in experiments with two groups is "repeated measure design" or "paired design". A paired design refers to studies where the two or more sets of measurements are taken from a single group of subjects under different conditions. Suppose we want to study the effect of sleep on memory. Having a test group of subjects who sleep normally and another group of subjects who are deprived of sleep does not reveal much about the target effect. Any observed difference may be due to the inherent difference in memory performance between these two groups. A repeated measure design is recommended here so that we can measure memory performance before and after sleep deprivation on the same group of subjects.
In the following, we illustrate how to conduct statistical tests in the unpaired design (i.e. test group vs control group) and in the paired design.
Unpaired (independent) group t-test
The unpaired t-test is applicable when the experimental group and the control group consist of different pools of subjects. Consider the following example:
Example Problem
A physiologist has conducted an experiment to evaluate the effect of hormone X on male sexual behavior. Ten rats were injected with hormone X and ten other rats received a placebo injection. Each rat was then housed with a female rat for 20 minutes, and the number of times each male mounted the female was counted. The test group had a sample mean number of mounts = 8.4 and a sample std. deviation = 6.197. The placebo group had a sample mean number of mounts = 5.6 and a sample std. deviation= 5.139.
Let's first identify the null hypothesis: The hormone has no effect on the number of times male rats mount a female during a 20 minute period. Note that we have 20 rats here divided into two groups. Such a design is an independent group design and an unpaired t-test is appropriate.
Solve the Problem by Hand
Now we test for a significant change in the mating rate of rats under the treatment of the hormone using an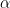 
= 0.05 significance level.
We define D0 as the difference in population means between the two conditions. The null hypothesis states that this value is 0:
H0: The hormone has no effect on the mating rate of rats (D0 = 0).
Then, calculate the difference in means of the two samples:
![\[
\bar{D} = \bar{x}_{hormone} - \bar{x}_{placebo} = 8.4-5.6=2.8
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_07da6ad44106ccdfc657c5c72152b9714d652950_p1.png "\[
\bar{D} = \bar{x}_{hormone} - \bar{x}_{placebo} = 8.4-5.6=2.8
\]")
and the standard error of the difference in means can be computed from the variance of each sample 
and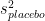 
:
![\[
se_{D} = \sqrt{\frac{s^{2}_{hormone} + s^{2}_{placebo}}{N}} = \sqrt{\frac{6.197^{2} + 5.139^{2}}{10}} = 2.546
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_97836081c3b05dbfad39e2117190e5a8276da8a4_p1.png "\[
se_{D} = \sqrt{\frac{s^{2}_{hormone} + s^{2}_{placebo}}{N}} = \sqrt{\frac{6.197^{2} + 5.139^{2}}{10}} = 2.546
\]")
Finally, we calculate the tobt. The formula is as follows:
![\[
t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.8 - 0}{2.546} = 1.10
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_6619a712e82713da89afea544926b1234ae93fe5_p1.png "\[
t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.8 - 0}{2.546} = 1.10
\]")
By looking up in the t distribution table, we find the 2-tailed t-critical value at df = 2N − 2 = 18 is 2.101. Since our obtained t-statistic is smaller than the critical value, we fail to reject the null hypothesis. The data do not support the hypothesis that hormone X has an effect on the frequency of male rat mounting behavior during a 20-minute period.
Note the degrees of freedom for an independent group design is the number of subjects minus 2.
Paired (repeated-measures) t-test
The paired group t-test is used when the two sets of measurements are taken on the same group of subjects. Consider the following example.
Example Problem
You are interested in determining whether an experimental birth control pill has the side effect of changing blood pressure. You randomly sample ten women from the city in which you live. You give five of them a placebo for a month and then measure their blood pressure. Then you switch them to the birth control pill for a month and again measure their blood pressure. The other five women receive the same treatment except that they are given the birth control pill first for a month, followed by the placebo for a month. The blood pressure readings are shown here.
Subject No. |
Placebo pill |
Birth Control pill |
1 |
102 |
108 |
2 |
76 |
76 |
3 |
66 |
69 |
4 |
71 |
78 |
5 |
68 |
74 |
6 |
85 |
85 |
7 |
82 |
79 |
8 |
78 |
78 |
9 |
79 |
80 |
10 |
80 |
81 |
The first step, again, is to identify the null hypothesis: The birth control pill does not affect the blood pressure of women who are taking it (i.e.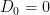 
). A two-tailed test should be used since an effect in either direction (i.e. whether the birth control pill increases or decreases blood pressure) would be of interest.
Solve the Problem by Hand
Now we test for a significant change in the blood pressure of women on birth control pills using an 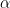= 0.05 significance level.
First, calculate the mean blood pressure change of the sample:
![\[
\bar{D} = 2.1
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_bc73b40c1e35fec2d60fbc5e3ee0dcb70e0e1c05_p1.png "\[
\bar{D} = 2.1
\]")
Next, the standard deviation of the sample difference scores (this is done by taking the differences first and then calculate the standard deviation):
s = 3.281
Now, the standard error of the mean sD>> is:
![\[
se_{D} = \frac{s}{\sqrt{n}} = \frac{3.281}{\sqrt{10}} = 1.038
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_aaa348b4639362e05b7dc65a7d9a33b3d844dcde_p1.png "\[
se_{D} = \frac{s}{\sqrt{n}} = \frac{3.281}{\sqrt{10}} = 1.038
\]")
Note that in the unpaired t-test, we calculated the standard error of the difference in means, while here we calculated the standard error of the mean difference. This is the key difference between the independent group design and the paired group design.
And, finally, our tobt:
![\[
t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.1 -0 }{1.038} = 2.024
\]](/StatsWiki/TwoSamplesOneVariable?action=AttachFile&do=get&target=latex_0b74d2db8cec79528dad21af50d60166896db4b6_p1.png "\[
t_{obt} = \frac{\bar{D}-D_0}{se_{D}} = \frac{2.1 -0 }{1.038} = 2.024
\]")
What is the degrees of freedom for a paired t-test? Since we only have 10 subjects in our group, the df is the same as in the one-sample t-test: N - 1. Now, we can look up the critical value of t for a two-tail test using the alpha value 0.05 and the appropriate degrees of freedom (df = 10-1 = 9). The critical value is 2.262, which is larger than our obtained t-statistic. Thus, we retain the null hypothesis and conclude that there is no sufficient evidence for the claim that the birth control pill affects the blood pressure of women who take it.
Note: If you used a statistics program to calculate the result of the t-test, you will find the p-value of this test is 0.074. When the p-value is greater than 0.05 and less than 0.1, we often refer to the result as "marginally significant". A marginally significant result often indicates a weak but probable effect, and thus is worth mentioning. Reporting a result as "marginally significant" is a common practice in experimental sciences.