Situations with Two or More Independent Variables of Interest
When considering the relationship among three or more variables, an interaction may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of multiple regression analyses, but they may also be evaluated using two-way ANOVA.
An Example Problem
To determine if prenatal exposure to cocaine alters dendritic spine density within prefrontal cortex, 20 rats were equally divided between treatment groups that were prenatally exposed to either cocaine or placebo. Further, because any effect of prenatal drug exposure might be evident at one age but not another, animals within each treatment group were further divided into two groups. One sub-group was studied at 4 weeks of age and the other was studied at 12 weeks of age. Thus, our independent variables are treatment (prenatal drug/placebo exposure) and age (lets say 4 and 12 weeks of age), and our dependent variable is spine density. The following table shows one possible outcome of such a study:
DENDRITIC SPINE DENSITY |
|||
4-Week Control |
4-Week Cocaine |
12-Week Control |
12-Week Cocaine |
7.5 |
5.5 |
8.0 |
5.0 |
8.0 |
3.5 |
10.0 |
4.5 |
6.0 |
4.5 |
13.0 |
4.0 |
7.0 |
6.0 |
9.0 |
6.0 |
6.5 |
5.0 |
8.5 |
4.0 |
There are three null hypotheses we may want to test. The first two test the effects of each independent variable (or factor) under investigation, and the third tests for an interaction between these two factors:
H01: Prenatal treatment substance (control or cocaine) has no effect on dendritic spine density in rats.
We can state this more formally as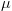 
Control = 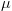Cocaine, where 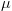Control and 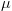Cocaine are the population mean spine densities of rats who were not and were prenatally exposed to cocaine, respectively.
H02: Age has no effect on dendritic spine density.
Or, more formally, 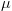4-Week = 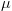12-Week, where 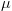4-Week and 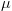12-Week are the population mean spine densities of rats at the ages of 4- and 12-weeks, respectively.
H03: The two factors (treatment and age) are independent; i.e., there is no interaction effect.
Or, 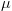4-Week, Control = 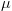4-Week, Cocaine = 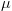12-Week, Control = 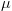12-Week, Cocaine, where each 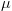represents the population mean spine density of rats at the labeled age and prenatal treatment condition.
Two-Way ANOVA
A two-way ANOVA is an analysis technique that quantifies how much of the variance in a sample can be accounted for by each of two categorical variables and their interactions. Note that different rats are used in each of the four experimental groups, so a standard two-way ANOVA should be used. If the same rats were used in each experimental condition, one would want to use a two-way repeated-measures ANOVA.
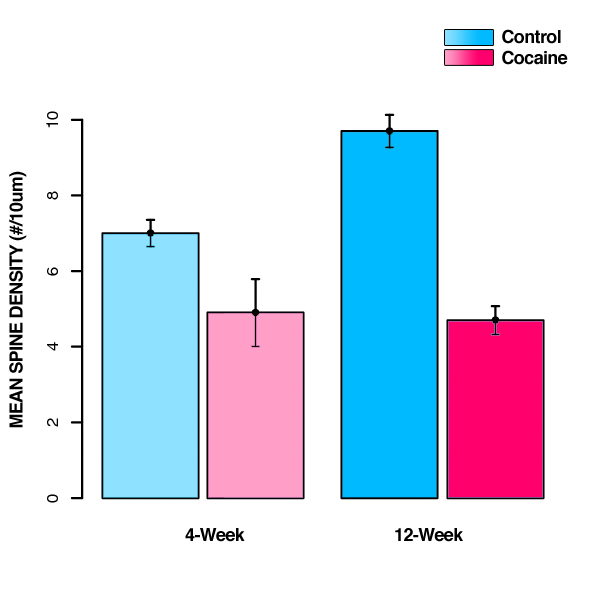
Step 1 is to compute group means (for each cell group), row and column means, and the grand mean (for all observations in the whole experiment):
GROUP MEANS |
|||
|
4-Week |
12-Week |
All Ages |
Control |
7 |
9.7 |
8.35 |
Cocaine |
4.9 |
4.7 |
4.8 |
All Prenatal Exposures |
5.95 |
7.2 |
6.575 |
Take a moment to define your variables
Before we go any further, we should define some variables that we'll use to complete the computations needed for the rest of the analysis:
n = number of observations in each group (here, it's 5 since there are 5 subjects per group)
N = total number of observations in the whole experiment (here, 20)
r = number of rows (here 2, one for each age group)
c = number of columns (here 2, one for each treatment substance condition
g = mean of a particular cell group g (for example, 12-Week, Control = 9.7).
R = mean of a particular row R (for example, 4-Week = 5.95)
C = mean of a particular column C (for example, Cocaine = 4.8)
And finally, to refer to the grand mean (the overall mean of all observations in the experiment), we'll simply use the notation (here, = 6.575).
Now that we've calculated all of our means, it would be helpful to also plot the mean data. (It's easier to understand it that way!)
Step 2 is to calculate the sum-of-squares for each individual group (SSg) using this:
![\[
SS = \sum_{i=1} (x_{i,g} - \overline{X}_g)^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_f69f0fdaf675e595f329938fb5a945e50c72d93d_p1.png "\[
SS = \sum_{i=1} (x_{i,g} - \overline{X}_g)^2
\]")
where xi,g is the ith measurement for group g, and g is the mean of group g. Remember here that when we say "group", we are referring to individual cells (not rows or columns, which we'll deal with next):
For each group, this formula is implemented as follows:
4-Week Control:
{7.5, 8, 6, 7, 6.5},
4-week, control = 7
SS4-week, control = (7.5-7)2 + (8-7)2 + (6-7)2 + (7-7)2 + (6.5-7)2 = 2.5
4-Week Cocaine:
{5.5, 3.5, 4.5, 6, 5},
4-week, cocaine = 4.9
SS4-week, cocaine = (5.5-4.9)2 + (3.5-4.9)2 + (4.5-4.9)2 + (6-4.9)2 + (5-4.9)2 = 3.7
12-Week Control:
{8, 10, 13, 9, 8.5},
12-week, control = 9.7
SS12-week, control = (8-9.7)2 + (10-9.7)2 + (13-9.7)2 + (9-9.7)2 + (8.5-9.7)2 = 15.8
12-Week Cocaine:
{5, 4.5, 4, 6, 4},
12-week, cocaine = 4.7
SS12-week, cocaine = (5-4.7)2 + (4.5-4.7)2 + (4-4.7)2 + (6-4.7)2 + (4-4.7)2 = 2.8
Step 3 is to calculate the between-groups sum-of-squares (SSB):
![\[
SS_B = n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_fbe398bc5e0bcdd916b5a33ab0662fac1026241a_p1.png "\[
SS_B = n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2
\]")
where n is the number of observations per group, g is the mean for group g, and is the grand mean. So...
SSB = n [(
4-week, control - )2 + ( 4-week, cocaine - )2 + ( 12-week, control - )2 + ( 12-week, cocaine - )2]
= 5 [(7 - 6.575 )2 + (4.9 - 6.575)2 + (9.7 - 6.575)2 + (4.7 - 6.575)2]
= 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]
= 5 [16.2675]
= 81.3375
Step 4 pertains to within-group variance. Here, we'll calculate the sum-of-squares, degrees of freedom, and mean square error within groups. First, compute the within-groups sum-of-squares (SSW) by summing the sum-of-squares you computed for each group in Step 1:
![\[
SS_W = \sum_{g} SS_g
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_4661d70fdac9a975e5dfe848b22a69a682186df1_p1.png "\[
SS_W = \sum_{g} SS_g
\]")
where SSg is the sum-of-squares for group g. So...
SSW = SS4-week, control + SS4-week, cocaine + SS12-week, control + SS12-week, cocaine
= 2.5 + 3.7 + 15.8 + 2.8
= 24.8
Next, calculate the within-groups degrees of freedom (dfW), using this:
dfW = N - rc
where Nis the total number of observations in the experiment, r is the number of rows, and c is the number of columns. So...
dfW = N - rc
= 20 - (2 * 2)
= 16
And finally, we compute the within-groups mean square error (sW2) by dividing SSWby dfW:
sW2 = SSW / dfW
= 24.8 / 16
= 1.55
Note that SSW is also known as the "residual" or "error" since it quantifies the amount of variability after the condition means are taken into account. The degrees of freedom here are N - rc because there are N data points, but the number of means fit is r*c, giving a total of N - rc variables that are free to vary.
Step 5 pertains to row variance. Here, we'll calculate all the same stuff we did in that last step (the sum-of-squares, degrees of freedom, and mean square error), but for the rows. First, compute the row sum-of-squares (SSR) by summing the sum-of-squares you computed for each row in Step 1:
![\[
SS_R = n_R \cdot \sum_{R} (\bar{X}_R - \bar{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_4371ee2c74ed3cc5239c3e6ad8a8e82f4a460bd6_p1.png "\[
SS_R = n_R \cdot \sum_{R} (\bar{X}_R - \bar{X})^2
\]")
where nR is the number of observations per row, R is the mean of row R, and is the grand mean.
SSR = nR [(
control - )2 + ( cocaine - )2]
= 10 [(8.35 - 6.575)2 + (4.8 - 6.575)2]
= 10 [3.150625 + 3.150625]
= 10 [6.30125]
= 63.0125
dfR = r - 1, where r is the number of rows.
= 2-1
= 1
And, just as before, divide the sum-of-squares by the degrees of freedom to get the mean square error for the rows:
sR2 = SSR / dfR
= 63.0125 / 1
= 63.0125
In Step 6, we calculate all of the variance metrics again for the columns (SSC, dfC, sC2):
![\[
SS_C = n_C \cdot \sum_{C} (\overline{X}_C - \overline{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_b56384377f49f594db2486f1026d6fe93e38e57a_p1.png "\[
SS_C = n_C \cdot \sum_{C} (\overline{X}_C - \overline{X})^2
\]")
where nC is the number of observations per column, C is the mean of column C, and is the grand mean. So...
SSC = nC (
4-week - )2 + ( 12-week - )2]
= 10 [(5.95 - 6.575)2 + (7.2 - 6.575)2]
= 10 [0.390625 + 0.390625]
= 10 [0.78125]
= 7.8125
dfC = c - 1, where c is the number of columns.
= 2-1
= 1
sC2 = SSC / dfC
= 7.8125 / 1
= 7.8125
Step 7 is to calculate the same three variance metrics the row-column interaction (SSRC, dfRC, sRC2). To calculateSSRC, simply sum the sum-of-squares you calculated for between-groups, rows, and columns (SSB, SSR, and SSC, respectively):
SSRC = SSB - SSR - SSC
= 81.3375 - 63.0125 - 7.8125
= 10.5125
And, for dfRC ...
dfRC = (r - 1)(c - 1)
= (2-1)(2-1)
= 1
Finally, sRC2:
sRC2 = SSRC / dfRC
= 10.5125 / 1
= 10.5125
Step 8 is to calculate the total variance metrics for the experiment. As always, start by computing the sum-of-squares (SST), which is done here by summing the between-groups, within-groups, row, column, and interaction sum-of-squares you computed in steps 3-7:
SST = SSB + SSW + SSR + SSC + SSRC
= 81.3375 + 24.8 + 63.0125 + 7.8125 + 10.5125
= 187.475
dfT = N - 1, where N is the total number of observations in the experiment.
= 20-1
= 19
Step 9 is calculating the F-values (Fobt) required to determine significance. For two-way ANOVAs, you'll compute 3 F-values: one for rows, one for columns, and one for the interaction between the two. Each F-value is computed by subtracting the mean square of the relevant dimension (R, C, or RC) by the within-groups mean square:
FR = sR2 / sW2
= 63.0125 / 1.55
= 40.65323
FC = sC2 / sW2
= 7.8125 / 1.55
= 5.040323
FRC = sRC2 / sW2
= 10.5125 / 1.55
= 6.782258
Step 10 is organizing all of the above calculations into a table, along with the appropriate Fcrit values (looked up in a table like this one). Then we'll compare eachFobt value we computed to the Fcrit values we looked up to draw our conclusions:
Fcrit (1, 16) α=0.5 = 4.49
ANOVA TABLE |
||||||
Source |
SS |
df |
s2 |
Fobt |
Fcrit |
p |
rows |
63.0125 |
1 |
63.0125 |
40.65323 |
4.49 |
p < 0.05 |
columns |
7.8125 |
1 |
7.8125 |
5.040323 |
4.49 |
p < 0.05 |
r * c |
10.5125 |
1 |
10.5125 |
6.782258 |
4.49 |
p < 0.05 |
within |
24.8 |
16 |
1.55 |
-- |
-- |
-- |
total |
187.475 |
19 |
-- |
-- |
-- |
-- |
Both variables (treatment and age) are significant, as indicated by the fact that Fobt > Fcrit for both. Thus, we can reject H01 and H02 and conclude that dendritic spine density is affected by prenatal cocaine exposure and age. The interaction between the two factors (r * c) is also significant. Thus, we can also reject H03 and conclude there is a significant interaction between treatment and age.
- To further interpret these results, we can plot the group means as follows:
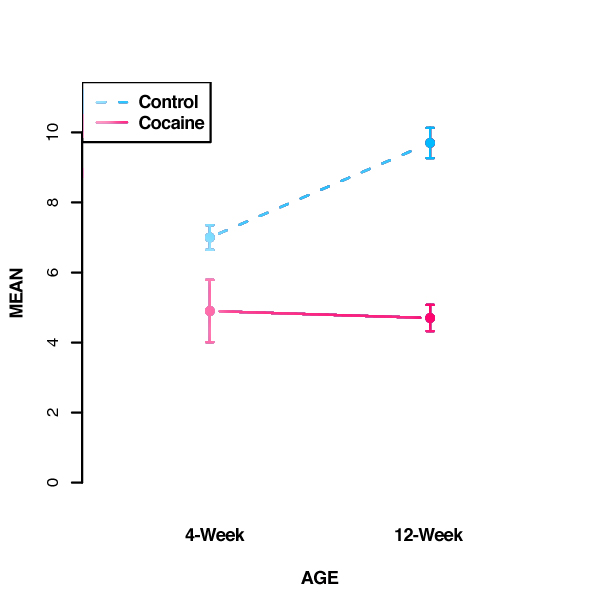
NOTE: Remember that the statistics provided by the ANOVA quantify the effect of each factor (in this case, treatment and age). These statistics do not compare individual condition means, such as whether 4-week control differs from 12-week control. If k = the number of groups, the number of possible comparisons is k * (k-1) / 2. In the above example, we have 4 groups, so there are (4*3)/2 = 6 possible comparisons between these group means. Statistical testing of these individual comparisons requires a post-hoc analysis that corrects for experiment-wise error rate. If all possible comparisons are of interest, the Tukey's HSD (Honestly Significant Difference) Test is commonly used.
Tukey's HSD (Honestly Significant Difference) Test
Tukey's test is a single-step, multiple-comparison statistical procedure often used in conjunction with an ANOVA to test which group means are significantly different from one another. It is used in cases where group sizes are equal (the Tukey-Kramer procedure is used if group sizes are unequal) and it compares all possible pairs of means. Note that the Tukey's test formula is very similar to that of the t-test, except that it corrects for experiment-wise error rate. (When there are multiple comparisons being made, the probability of making a type I error (rejecting a true null hypothesis) increases, so Tukey's test corrects for this.) The formula for a Tukey's test is:
![\[
q_{obt} = (Y_{A} - Y_{B}) / \sqrt{ s_{W}^2 / n}
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_51b588f7c3115f85a29b1bd8bc32f7b8a737fe15_p1.png "\[
q_{obt} = (Y_{A} - Y_{B}) / \sqrt{ s_{W}^2 / n}
\]")
where YA is the larger of the two means being compared, YB is the smaller,sW2 is the mean squared error within, and n is the number of data points within each group . Once computed, the qobt value is compared to a q-value from the q distribution. If the qobt value is larger than the qcrit value from the distribution, the two means are significantly different.
So, if we wanted to use a Tukey's test to determine whether 4-week control significantly differs from 12-week control, we'd calculate it as follows
qobt =
12-week, control - 4-week, control /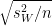 
= 9.7 - 7 /
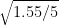
= 9.7 - 7 /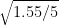
= 2.7 / 0.5567764
= 4.849343
The qcrit value may be looked up in a chart (like this one) using the appropriate values for k (which represents the number of group means, so 4 here) and dfw (16). So here, qcrit (4, 16) α=0.5= 4.05. Since qobt > qcrit (4.85 > 4.05), we can conclude that the two means are, in fact, (honestly) significantly different.
Additional group comparisons reveal that spine density does not change significantly with age in the cocaine-exposed group, but is significantly greater in the control group as compared to cocaine-exposed animals at both 4 and 12 weeks of age. Thus, the effect of prenatal drug exposure is magnified with time due to a developmental increase in spine density that occurs only in the control group.
IMPORTANT NOTE: There are various post-hoc tests that can be used, and the choice of which method to apply is a controversial area in statistics. The different tests vary in how conservative they are: more conservative tests are less powerful and have a lower risk of a type I error (rejecting a true null hypothesis), however this comes at the cost of increasing the risk of a type II error (incorrectly accepting the null hypothesis). Some common methods, listed in order of decreasing power, are: Fisher’s LSD, Newman-Keuls, Tukey HSD, Bonferonni, Scheffé. The following provides some guidelines for choosing an appropriate post-hoc procedure.
If all pairwise comparisons are truly relevant, the Tukey method is recommended.
If it is most reasonable to compare all groups against a single control, then the Dunnett test is recommended.
If only a subset of the pairwise comparisons are relevant, then the Bonferroni method is often utilized for those selected comparisons. For example, in the present example one would likely not be interested in comparing the 4-week control to the 12-week cocaine group, or the 12-week control to the 4-week cocaine group.
Multiple Regression
Another analysis technique you could use is a multiple regression. In multiple regression, we find coefficients for each group such that we are able to best predict the group means. The multiple regression computes standard errors on the coefficients, meaning that we can determine if a coefficient is significantly different from zero. On this simple example, multiple regression will give identical answers to ANOVA, but in more complex cases, multiple regression is a more powerful technique that allows you to include additional nuisance predictors, that the analysis controls for before testing for significance of your independent variables.