|
Size: 1670
Comment:
|
Size: 11630
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| When considering the relationship among three or more variables, an '''interaction''' may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of regression analyses, but they may also be evaluated using two-way ANOVA. A simple setting in which interactions can arise is a two-factor experiment analyzed using Analysis of Variance (ANOVA). Suppose we are interested in studying the effects of cocaine on sleep. We might design an experiment to simultaneously test whether both the use of cocaine and the duration of usage affect the number of hours a squirrel will sleep in a night. We might give half of the squirrels we test cocaine, and the other half a placebo (control) substance (the ''substance variable''). And we might vary the duration of usage by administering cocaine or placebo for one of two possible durations before test, 4 weeks or 12 weeks (the ''usage duration variable''). || 4-Week Control || 4-Week Cocaine || 12-Week Control || 12-Week Cocaine || |
= Situations with more than two variables of interest = When considering the relationship among three or more variables, an '''interaction''' may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of '''Multiple Regression''' analyses, but they may also be evaluated using '''Two-Way ANOVA'''. * [[MoreThanTwoVariables#An Example Problem|Example Problem]] * [[MoreThanTwoVariables#Two-Way ANOVA|Two-Way ANOVA]] * [[MoreThanTwoVariables#Multiple Regression|Multiple Regression]] == An Example Problem == To Measures of spine density were taken from both control (Cntl) and experimental (Coc: prenatal cocaine exposure) rats at 4 and 12 weeks of age. Suppose we want to determine if prenatal exposure to cocaine alters dendritic spine density in prefrontal cortex over the course of development. We might design an experiment to simultaneously test whether prenatal exposure to cocaine and age affects the dendritic spine density in rats of two different ages. Suppose we took 20 rats, half of which were exposed to cocaine prenatally (the ''cocaine'' group) and half of which were not (the ''control'' group). We'll refer to the difference between these two groups (''cocaine'' vs. ''control'') as the ''prenatal-exposure'' variable. Now further suppose that each prenatal-exposure group is composed of an equal number of rats of two different ages: either 4-weeks or 12-weeks. We can refer to this difference as the ''age'' variable. We can then consider the average response of our dependent variable (e.g. dendritic spine density) for each rat, as a function of both variables (e.g. prenatal-exposure and age). The following table shows one possible outcome of such a study: ||||||||DENDRITIC SPINE DENSITY|| || '''4-Week Control''' || '''4-Week Cocaine''' || '''12-Week Control''' || '''12-Week Cocaine''' || |
| Line 12: | Line 26: |
have two binary factors A and B. For example, these factors might indicate whether a treatment was administered to a patient, and for how long the treatment was used. We can then consider the average treatment response (e.g. the symptom levels following treatment) for each patient, as a function of the treatment combination that was administered. The following table shows one possible situation: |
There are '''three null hypotheses''' we may want to test. The first two test the effects of each variable (or factor) under investigation: * H,,01,,: Both prenatal-exposure groups have the same dendritic spine density on average. * H,,02,,: Both age groups have the same dendritic spine density on average. And the third tests for an interaction between these two factors: * H,,03,,: The two factors (pre-natal exposure and age) are independent or there is no interaction effect. == Two-Way ANOVA == A two-way ANOVA is an analysis technique that quantifies how much of the variance in a sample can be accounted for by each of two categorical variables and their interactions. '''Step 1''' is to compute the '''group means''' (for each cell, row, and column): ||||||||GROUP MEANS|| || || '''4-Week''' || '''12-Week''' || '''''All Ages''''' || || '''Control''' || 7 || 9.7|| ''8.35'' || || '''Cocaine''' || 4.9 || 4.7 || ''4.8'' || || '''''All Prenatal Exposures''''' || ''5.95'' || ''7.2'' || ''6.575'' || It's important to plot the numbers--it's easier to understand them that way: {{attachment:o.png|Means by group|width=450}} '''Step 2''' is to calculate the sum of squares (SS) for each group (cell) using the following formula: {{{#!latex \[ \sum_{i=1} (x_{i,g} - \overline{X}_g)^2 \] }}} where <<latex($x_{i,g}$)>> is the i'th measurement for group g, and <<latex($\overline{X}_g$)>> is the overall group mean for group g. For each group, this formula is implemented as follows: 4-Week Control: <<BR>> {7.5, 8, 6, 7, 6.5}, <<latex($\overline{X}_{4-week, control}$)>> = 7<<BR>> <<latex($SS_{4-week, control}$)>> = (7.5-7)^2^ + (8-7)^2^ + (6-7)^2^ + (7-7)^2^ + (6.5-7)^2^ = '''2.5'''<<BR>><<BR>> 4-Week Cocaine: <<BR>> {5.5, 3.5, 4.5, 6, 5}, <<latex($\overline{X}_{4-week, cocaine}$)>> = 4.9<<BR>> <<latex($SS_{4-week, cocaine}$)>> = (5.5-4.9)^2^ + (3.5-4.9)^2^ + (4.5-4.9)^2^ + (6-4.9)^2^ + (5-4.9)^2^ = '''3.7'''<<BR>><<BR>> 12-Week Control: <<BR>> {8, 10, 13, 9, 8.5}, <<latex($\overline{X}_{12-week, control}$)>> = 9.7<<BR>> <<latex($SS_{12-week, control}$)>> = (8-9.7)^2^ + (10-9.7)^2^ + (13-9.7)^2^ + (9-9.7)^2^ + (8.5-9.7)^2^ = '''15.8'''<<BR>><<BR>> 12-Week Cocaine: <<BR>> {5, 4.5, 4, 6, 4}, <<latex($\overline{X}_{12-week, cocaine}$)>> = 4.7<<BR>> <<latex($SS_{12-week, cocaine}$)>> = (5-4.7)^2^ + (4.5-4.7)^2^ + (4-4.7)^2^ + (6-4.7)^2^ + (4-4.7)^2^ = '''2.8'''<<BR>><<BR>> '''Step 3''' is to calculate the between-groups sum of squares(''SS,,B,,''):<<BR>> {{{#!latex \[ n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2 \] }}} where n is the number of subjects in each group, <<latex($\overline{X}_g$)>> is the mean for group g, and <<latex($\overline{X}$)>> is the overall mean (across groups). <<latex($SS_{B}$)>> = <<latex($n$)>> [( <<latex($\overline{X}_{4-week, control}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{4-week, cocaine}$)>> - <<latex($\overline{X}$)>>)^2^ + ( <<latex($\overline{X}_{12-week, control}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{12-week, cocaine}$)>> - <<latex($\overline{X}$)>>)^2^]<<BR>> = 5 [(7 - 6.575 )^2^ + (4.9 - 6.575)^2^ + (9.7 - 6.575)^2^ + (4.7 - 6.575)^2^]<<BR>> = 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]<<BR>> = 5 [16.2675]<<BR>> = '''81.3375'''<<BR>><<BR>> Now, '''Step 4''' , we'll calculate the sum-of-squares within groups (<<latex($SS_{W}$)>>). For a group g, this is {{{#!latex \[ \sum_{g} SS_g \] }}} So: <<BR>> <<latex($SS_{W}$)>> = <<latex($SS_{4-week, control}$)>> + <<latex($SS_{4-week, cocaine}$)>> + <<latex($SS_{12-week, control}$)>> + <<latex($SS_{12-week, cocaine}$)>><<BR>> = 2.5 + 3.7 + 15.8 + 2.8<<BR>> = '''24.8'''<<BR>><<BR>> <<latex($df_{w}$)>> = <<latex($N - rc$)>><<BR>> = 20 - (2 * 2)<<BR>> = 16<<BR>><<BR>> <<latex($s_{W}$)>>^2^ = <<latex($SS_{W}$)>> / <<latex($df_{w}$)>><<BR>> = 24.8 / 16<<BR>> = '''1.55'''<<BR>><<BR>> For '''Step 5''', we'll calculate the sum-of-squares for the rows (<<latex($SS_{R}$)>>):<<BR>> {{{#!latex \[ \sum_{r} (\overline{X}_r - \overline{X})^2 \] }}} where r ranges over rows. <<latex($SS_{R}$)>> = <<latex($n$)>> [( <<latex($\overline{X}_{control}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{cocaine}$)>> - <<latex($\overline{X}$)>>)^2^]<<BR>> = 10 [(8.35 - 6.575)^2^ + (4.8 - 6.575)^2^]<<BR>> = 10 [3.150625 + 3.150625]<<BR>> = 10 [6.30125]<<BR>> = '''63.0125'''<<BR>><<BR>> '''''df,,R,,''''' = ''r'' - 1<<BR>> = 2-1<<BR>> = '''1'''<<BR>><<BR>> '''''s,,R,,^2^''''' = ''SS,,R,,'' / ''df,,R,,''<<BR>> = 63.0125 / 1<<BR>> = '''63.0125'''<<BR>><<BR>> In '''Step 6''', we calculate the sum-of-squares for the columns (<<latex($SS_{C}$)>>):<<BR>> {{{#!latex \[ \sum_{c} (\overline{X}_c - \overline{X})^2 \] }}} where c ranges over columns. <<latex($SS_{C}$)>> = <<latex($n$)>> ( <<latex($\overline{X}_{4-week}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{12-week}$)>> - <<latex($\overline{X}$)>> )^2^]<<BR>> = 10 [(5.95 - 6.575)^2^ + (7.2 - 6.575)^2^]<<BR>> = 10 [0.390625 + 0.390625]<<BR>> = 10 [0.78125]<<BR>> = '''7.8125'''<<BR>><<BR>> '''''df,,C,,''''' = ''c'' - 1<<BR>> = 2-1<<BR>> = '''1'''<<BR>><<BR>> '''''s,,C,,^2^''''' = ''SS,,C,,'' / ''df,,C,,''<<BR>> = 7.8125 / 1<<BR>> = '''7.8125'''<<BR>><<BR>> In '''Step 7''', calculate the sum-of-squares for the interaction (<<latex($SS_{RC}$)>>):<<BR>> '''''SS,,RC,,''''' = ''SS,,B,,'' - ''SS,,R,,'' - ''SS,,C,,''<<BR>> = 81.3375 - 63.0125 - 7.8125<<BR>> = 10.5125<<BR>><<BR>> '''''df,,RC,,''''' = (''r'' - 1)(''c'' - 1)<<BR>> = (2-1)(2-1)<<BR>> = '''1'''<<BR>><<BR>> '''''s,,RC,,^2^''''' = ''SS,,RC,,'' / ''df,,RC,,''<<BR>> = 10.5125 / 1<<BR>> = '''10.5125'''<<BR>><<BR>> Now, in '''Step 8''', we'll calculate the total sum-of-squares (<<latex($SS_{T}$)>>):<<BR>> '''''SS,,T,,''''' = ''SS,,B,,'' + ''SS,,W,,'' + ''SS,,R,,'' + ''SS,,C,,'' + ''SS,,RC,,''<<BR>> = 81.3375 + 24.8 + 63.0125 + 7.8125 + 10.5125<<BR>> = 187.475<<BR>><<BR>> '''''df,,T,,''''' = ''N'' - 1<<BR>> = 20-1<<BR>> = '''19'''<<BR>><<BR>> At '''Step 9''', we calculate the ''F'' values: '''''F,,R,,''''' = ''s,,R,,^2^'' / ''s,,W,,^2^''<<BR>> = 63.0125 / 1.55<<BR>> = '''40.65323'''<<BR>><<BR>> '''''F,,C,,''''' = ''s,,C,,^2^'' / ''s,,W,,^2^''<<BR>> = 7.8125 / 1.55<<BR>> = '''5.040323'''<<BR>><<BR>> '''''F,,RC,,''''' = ''s,,RC,,^2^'' / ''s,,W,,^2^''<<BR>> = 10.5125 / 1.55<<BR>> = '''6.782258'''<<BR>><<BR>> And, finally, at '''Step 10''', we can organize all of the above into a table, along with the appropriate '''F,,CRIT,,''' values (looked up in a table like [[http://www.medcalc.org/manual/f-table.php|this one]]) that we'll use for comparison and interpretation of our computations: '''F,,CRIT,,''' (1, 16) ,,α=0.5,, = '''4.49''' |||||||||||||| ANOVA TABLE || || '''''Source''''' || '''''SS''''' || '''''df''''' || '''''s^2^''''' || '''''F,,obt,,''''' || '''''F,,crit,,''''' || '''''p''''' || || rows || 63.0125 || 1 || 63.0125 || 40.65323 || 4.49 || ''p'' < 0.05 || || columns || 7.8125 || 1 || 7.8125 || 5.040323 || 4.49 || ''p'' < 0.05 || || r * c || 10.5125 || 1 || 10.5125 || 6.782258 || 4.49 || ''p'' < 0.05 || || within || 24.8 || 16 || 1.55 || -- || -- || -- || || total || 187.475 || 19 || -- || -- || -- || -- || Both factors (prenatal-exposure and age) are significant, as indicate by the fact that '''F,,OBT,,''' > '''F,,CRIT,,'''. Thus, we can reject all H,,01,, and H,,02,, and conclude that dendritic spine density is affected by prenatal exposure and age. The interaction between the two factors (r * c) is also significant. Thus, we can also reject H,,03,, and conclude there is a significant interaction between these two factors. To further interpret these results, we can plot the group means as follows: {{attachment:crossover.png|Means by group|width=450}} So, as indicated above, spine density is significantly greater in the control group as compared to drug-exposed animals at both 4 and 12 weeks of age. The effect of prenatal drug exposure is magnified with time due to a developmental increase in spine density that occurs only in the control group. Between 4 and 12 weeks of age, spine density in prefrontal cortex increases significantly in control animals, while it remains relatively unchanged in the drug-exposed animals. == Multiple Regression == Another analysis technique you could use is a multiple regression. In multiple regression, we find coefficients for each group such that we are able to best predict the group means. The multiple regression computes standard errors on the coefficients, meaning that we can determine if a coefficient is significantly different from zero. On this simple example, multiple regression will give identical answers to ANOVA, but in more complex cases, multiple regression is a more powerful technique that allows you to include additional nuisance predictors, that the analysis controls for before testing for significance of your independent variables. |
Situations with more than two variables of interest
When considering the relationship among three or more variables, an interaction may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of Multiple Regression analyses, but they may also be evaluated using Two-Way ANOVA.
An Example Problem
To Measures of spine density were taken from both control (Cntl) and experimental (Coc: prenatal cocaine exposure) rats at 4 and 12 weeks of age.
Suppose we want to determine if prenatal exposure to cocaine alters dendritic spine density in prefrontal cortex over the course of development. We might design an experiment to simultaneously test whether prenatal exposure to cocaine and age affects the dendritic spine density in rats of two different ages. Suppose we took 20 rats, half of which were exposed to cocaine prenatally (the cocaine group) and half of which were not (the control group). We'll refer to the difference between these two groups (cocaine vs. control) as the prenatal-exposure variable. Now further suppose that each prenatal-exposure group is composed of an equal number of rats of two different ages: either 4-weeks or 12-weeks. We can refer to this difference as the age variable. We can then consider the average response of our dependent variable (e.g. dendritic spine density) for each rat, as a function of both variables (e.g. prenatal-exposure and age). The following table shows one possible outcome of such a study:
DENDRITIC SPINE DENSITY |
|||
4-Week Control |
4-Week Cocaine |
12-Week Control |
12-Week Cocaine |
7.5 |
5.5 |
8.0 |
5.0 |
8.0 |
3.5 |
10.0 |
4.5 |
6.0 |
4.5 |
13.0 |
4.0 |
7.0 |
6.0 |
9.0 |
6.0 |
6.5 |
5.0 |
8.5 |
4.0 |
There are three null hypotheses we may want to test. The first two test the effects of each variable (or factor) under investigation:
H01: Both prenatal-exposure groups have the same dendritic spine density on average.
H02: Both age groups have the same dendritic spine density on average.
And the third tests for an interaction between these two factors:
H03: The two factors (pre-natal exposure and age) are independent or there is no interaction effect.
Two-Way ANOVA
A two-way ANOVA is an analysis technique that quantifies how much of the variance in a sample can be accounted for by each of two categorical variables and their interactions.
Step 1 is to compute the group means (for each cell, row, and column):
GROUP MEANS |
|||
|
4-Week |
12-Week |
All Ages |
Control |
7 |
9.7 |
8.35 |
Cocaine |
4.9 |
4.7 |
4.8 |
All Prenatal Exposures |
5.95 |
7.2 |
6.575 |
It's important to plot the numbers--it's easier to understand them that way:
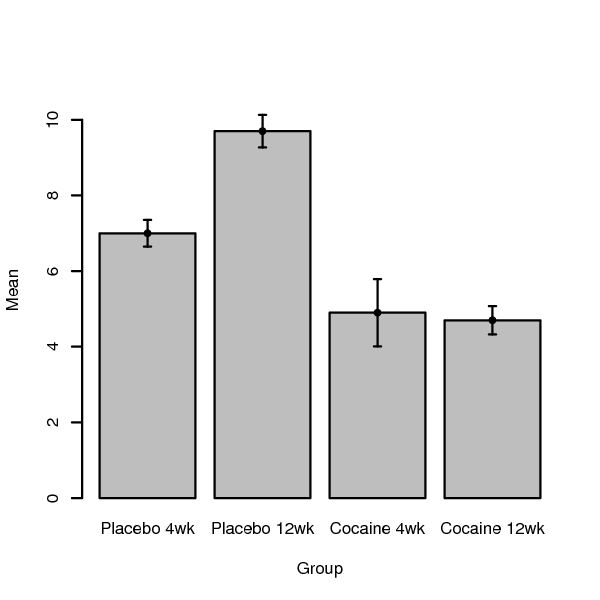
Step 2 is to calculate the sum of squares (SS) for each group (cell) using the following formula:
![\[
\sum_{i=1} (x_{i,g} - \overline{X}_g)^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_9d9baaf8628df39274fe16b1d33167495cb3492f_p1.png "\[
\sum_{i=1} (x_{i,g} - \overline{X}_g)^2
\]")
where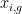 
is the i'th measurement for group g, and 
is the overall group mean for group g.
For each group, this formula is implemented as follows:
4-Week Control:
{7.5, 8, 6, 7, 6.5},
= 7
= (7.5-7)2 + (8-7)2 + (6-7)2 + (7-7)2 + (6.5-7)2 = 2.5
4-Week Cocaine:
{5.5, 3.5, 4.5, 6, 5},
= 4.9
= (5.5-4.9)2 + (3.5-4.9)2 + (4.5-4.9)2 + (6-4.9)2 + (5-4.9)2 = 3.7
12-Week Control:
{8, 10, 13, 9, 8.5},
= 9.7
= (8-9.7)2 + (10-9.7)2 + (13-9.7)2 + (9-9.7)2 + (8.5-9.7)2 = 15.8
12-Week Cocaine:
{5, 4.5, 4, 6, 4},
= 4.7
= (5-4.7)2 + (4.5-4.7)2 + (4-4.7)2 + (6-4.7)2 + (4-4.7)2 = 2.8
Step 3 is to calculate the between-groups sum of squares(SSB):
![\[
n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_502a12ddb5e68a9b8c67ce461d55b4984a724b6c_p1.png "\[
n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2
\]")
where n is the number of subjects in each group, is the mean for group g, and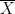 
is the overall mean (across groups).
= 
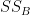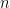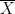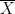[( - )2 + ( - 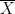)2 + ( - 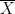)2 + ( - )2]
= 5 [(7 - 6.575 )2 + (4.9 - 6.575)2 + (9.7 - 6.575)2 + (4.7 - 6.575)2]
= 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]
= 5 [16.2675]
= 81.3375
Now, Step 4 , we'll calculate the sum-of-squares within groups (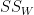
). For a group g, this is
![\[
\sum_{g} SS_g
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_36f2ee092d87df367fe63de62ab54636d2ae4899_p1.png "\[
\sum_{g} SS_g
\]")
So:
- = + + +
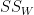= 2.5 + 3.7 + 15.8 + 2.8
= 24.8
= 
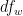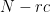
= 20 - (2 * 2)
= 16
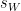2 = /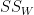
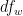
= 24.8 / 16
= 1.55
For Step 5, we'll calculate the sum-of-squares for the rows (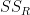
):
![\[
\sum_{r} (\overline{X}_r - \overline{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_6929f987075c55537ae0d762054416fa3bc7c463_p1.png "\[
\sum_{r} (\overline{X}_r - \overline{X})^2
\]")
where r ranges over rows.
- = [(
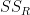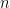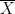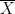- )2 + ( 
- )2]
= 10 [(8.35 - 6.575)2 + (4.8 - 6.575)2]
= 10 [3.150625 + 3.150625]
= 10 [6.30125]
= 63.0125
dfR = r - 1
= 2-1
= 1
sR2 = SSR / dfR
= 63.0125 / 1
= 63.0125
In Step 6, we calculate the sum-of-squares for the columns (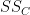
):
![\[
\sum_{c} (\overline{X}_c - \overline{X})^2
\]](/StatsWiki/MoreThanTwoVariables?action=AttachFile&do=get&target=latex_ab08df449ae94e386b5c1b5207e8983ee723253f_p1.png "\[
\sum_{c} (\overline{X}_c - \overline{X})^2
\]")
where c ranges over columns.
- = (
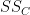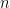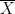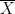- )2 + ( 
- )2]
= 10 [(5.95 - 6.575)2 + (7.2 - 6.575)2]
= 10 [0.390625 + 0.390625]
= 10 [0.78125]
= 7.8125
dfC = c - 1
= 2-1
= 1
sC2 = SSC / dfC
= 7.8125 / 1
= 7.8125
In Step 7, calculate the sum-of-squares for the interaction (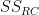
):
SSRC = SSB - SSR - SSC
= 81.3375 - 63.0125 - 7.8125
= 10.5125
dfRC = (r - 1)(c - 1)
= (2-1)(2-1)
= 1
sRC2 = SSRC / dfRC
= 10.5125 / 1
= 10.5125
Now, in Step 8, we'll calculate the total sum-of-squares (
):
SST = SSB + SSW + SSR + SSC + SSRC
= 81.3375 + 24.8 + 63.0125 + 7.8125 + 10.5125
= 187.475
dfT = N - 1
= 20-1
= 19
At Step 9, we calculate the F values:
FR = sR2 / sW2
= 63.0125 / 1.55
= 40.65323
FC = sC2 / sW2
= 7.8125 / 1.55
= 5.040323
FRC = sRC2 / sW2
= 10.5125 / 1.55
= 6.782258
And, finally, at Step 10, we can organize all of the above into a table, along with the appropriate FCRIT values (looked up in a table like this one) that we'll use for comparison and interpretation of our computations:
FCRIT (1, 16) α=0.5 = 4.49
ANOVA TABLE |
||||||
Source |
SS |
df |
s2 |
Fobt |
Fcrit |
p |
rows |
63.0125 |
1 |
63.0125 |
40.65323 |
4.49 |
p < 0.05 |
columns |
7.8125 |
1 |
7.8125 |
5.040323 |
4.49 |
p < 0.05 |
r * c |
10.5125 |
1 |
10.5125 |
6.782258 |
4.49 |
p < 0.05 |
within |
24.8 |
16 |
1.55 |
-- |
-- |
-- |
total |
187.475 |
19 |
-- |
-- |
-- |
-- |
Both factors (prenatal-exposure and age) are significant, as indicate by the fact that FOBT > FCRIT. Thus, we can reject all H01 and H02 and conclude that dendritic spine density is affected by prenatal exposure and age. The interaction between the two factors (r * c) is also significant. Thus, we can also reject H03 and conclude there is a significant interaction between these two factors.
- To further interpret these results, we can plot the group means as follows:
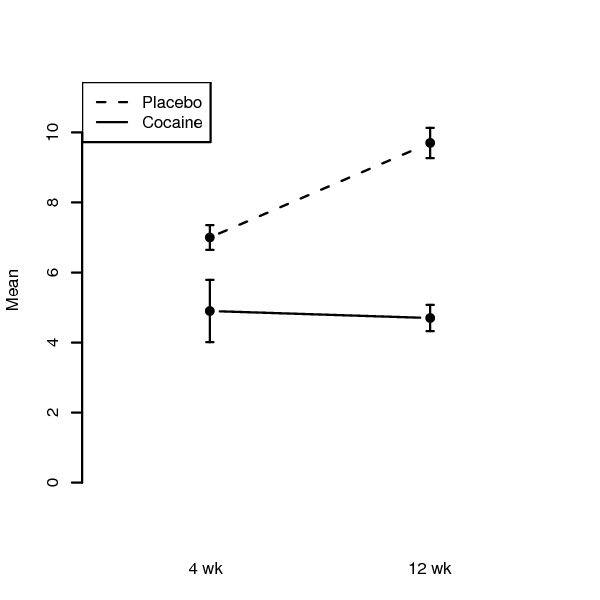
So, as indicated above, spine density is significantly greater in the control group as compared to drug-exposed animals at both 4 and 12 weeks of age. The effect of prenatal drug exposure is magnified with time due to a developmental increase in spine density that occurs only in the control group. Between 4 and 12 weeks of age, spine density in prefrontal cortex increases significantly in control animals, while it remains relatively unchanged in the drug-exposed animals.
Multiple Regression
Another analysis technique you could use is a multiple regression. In multiple regression, we find coefficients for each group such that we are able to best predict the group means. The multiple regression computes standard errors on the coefficients, meaning that we can determine if a coefficient is significantly different from zero. On this simple example, multiple regression will give identical answers to ANOVA, but in more complex cases, multiple regression is a more powerful technique that allows you to include additional nuisance predictors, that the analysis controls for before testing for significance of your independent variables.