Differences between revisions 137 and 138

Situations with more than two variables of interest

When considering the relationship among three or more variables, an interaction may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of Multiple Regression analyses, but they may also be evaluated using Two-Way ANOVA.

An Example Problem

Suppose we want to determine if prenatal exposure to cocaine alters dendritic spine density in prefrontal cortex over the course of development. We might design an experiment to simultaneously test whether prenatal exposure to cocaine and age affect the dendritic spine density in rats. Suppose we took 20 rats, half of which were exposed to cocaine prenatally (the cocaine group) and half of which were not (the control group). We'll refer to the difference between these two groups (cocaine vs. control) as the prenatal-exposure variable. Now further suppose that each prenatal-exposure group is composed of an equal number of rats of two different ages: either 4-weeks or 12-weeks. We can refer to this difference as the age variable. We can then consider the average response of our dependent variable (e.g. dendritic spine density) for each rat, as a function of both variables (e.g. prenatal-exposure and age). The following table shows one possible outcome of such a study:

DENDRITIC SPINE DENSITY
4-Week Control	4-Week Cocaine	12-Week Control	12-Week Cocaine
7.5	5.5	8.0	5.0
8.0	3.5	10.0	4.5
6.0	4.5	13.0	4.0
7.0	6.0	9.0	6.0
6.5	5.0	8.5	4.0

There are three null hypotheses we may want to test. The first two test the effects of each variable (or factor) under investigation:

H₀₁: Both prenatal-exposure groups have the same dendritic spine density on average.
H₀₂: Both age groups have the same dendritic spine density on average.

And the third tests for an interaction between these two factors:

H₀₃: The two factors (pre-natal exposure and age) are independent or there is no interaction effect.

Two-Way ANOVA

A two-way ANOVA is an analysis technique that quantifies how much of the variance in a sample can be accounted for by each of two categorical variables and their interactions.

Step 1 is to compute the group means (for each cell, row, and column):

GROUP MEANS
	4-Week	12-Week	All Ages
Control	7	9.7	8.35
Cocaine	4.9	4.7	4.8
All Prenatal Exposures	5.95	7.2	6.575

It's important to plot the numbers--it's easier to understand them that way:

Means by group

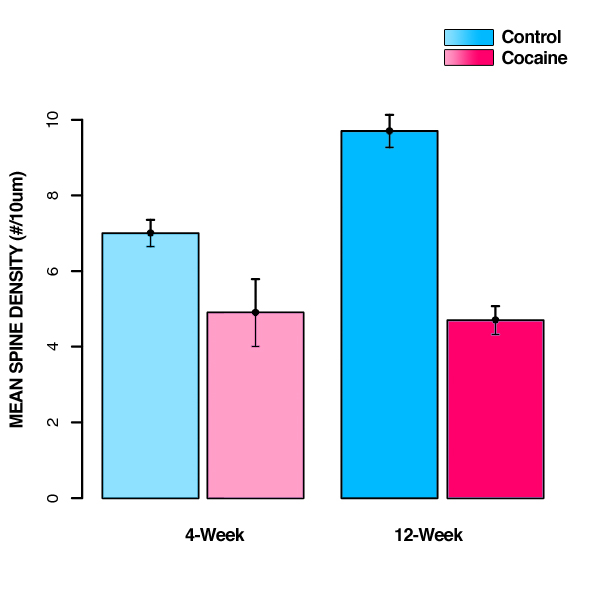
Step 2 is to calculate the sum of squares (SS) for each group (cell) using the following formula:

$\sum_{i=1} (x_{i,g} - \overline{X}_g)^2$

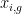where $x_{i,g}$ is the i'th measurement for group g, and $\overline{X}_g$ is the overall group mean for group g.

For each group, this formula is implemented as follows:

4-Week Control:
- {7.5, 8, 6, 7, 6.5}, $\overline{X}_{4-week, control}$ = 7
  $SS_{4-week, control}$ = (7.5-7)² + (8-7)² + (6-7)² + (7-7)² + (6.5-7)² = 2.5
4-Week Cocaine:
- {5.5, 3.5, 4.5, 6, 5}, $\overline{X}_{4-week, cocaine}$ = 4.9
  $SS_{4-week, cocaine}$ = (5.5-4.9)² + (3.5-4.9)² + (4.5-4.9)² + (6-4.9)² + (5-4.9)² = 3.7
12-Week Control:
- {8, 10, 13, 9, 8.5}, $\overline{X}_{12-week, control}$ = 9.7
  $SS_{12-week, control}$ = (8-9.7)² + (10-9.7)² + (13-9.7)² + (9-9.7)² + (8.5-9.7)² = 15.8
12-Week Cocaine:
- {5, 4.5, 4, 6, 4}, $\overline{X}_{12-week, cocaine}$ = 4.7
  $SS_{12-week, cocaine}$ = (5-4.7)² + (4.5-4.7)² + (4-4.7)² + (6-4.7)² + (4-4.7)² = 2.8

Step 3 is to calculate the between-groups sum of squares(SS_B):

$n \cdot \sum_{g} (\overline{X}_{g} - \overline{X})^2$

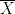where n is the number of subjects in each group, $\overline{X}_g$ is the mean for group g, and $\overline{X}$ is the overall mean (across groups).

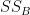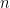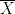$SS_{B}$ = [( $\overline{X}_{4-week, control}$ - $\overline{X}$ )² + ( $\overline{X}_{4-week, cocaine}$ - $\overline{X}$ )² + ( $\overline{X}_{12-week, control}$ - $\overline{X}$ )² + ( $\overline{X}_{12-week, cocaine}$ - $\overline{X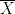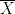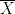}$ )²]
- = 5 [(7 - 6.575 )² + (4.9 - 6.575)² + (9.7 - 6.575)² + (4.7 - 6.575)²]
  = 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]
  = 5 [16.2675]
  = 81.3375

Now, Step 4 , we'll calculate the sum-of-squares within groups (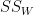 $SS_{W}$ ). For a group g, this is

$\sum_{g} SS_g$

So:

$SS_{W}$ = $SS_{4-week, control}$ + $SS_{4-week, cocaine}$ + $SS_{12-week, control}$ + $SS_{12-week, cocaine}$
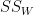- = 2.5 + 3.7 + 15.8 + 2.8
  = 24.8
$df_{w}$ =
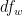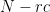
- = 20 - (2 * 2)
  = 16
$s_{W}$ ² = $SS_{W}$ / $df_{w}$
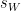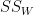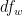
- = 24.8 / 16
  = 1.55

Note that 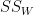$SS_{W}$ is also known as the "residual" or "error" since it quantifies the amount of variability after the condition means are taken into account. The degrees of freedom here are N-rc because there are N data points, but the number of means fit is r*c, giving a total of N-rc variables that are free to vary.

For Step 5, we'll calculate the sum-of-squares for the rows (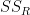 $SS_{R}$ ):

$\sum_{r} (\overline{X}_r - \overline{X})^2$

where r ranges over rows.

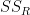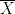$SS_{R}$ = [( $\overline{X}_{control}$ - $\overline{X}$ )² + ( $\overline{X}_{cocaine}$ - $\overline{X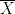}$ )²]
- = 10 [(8.35 - 6.575)² + (4.8 - 6.575)²]
  = 10 [3.150625 + 3.150625]
  = 10 [6.30125]
  = 63.0125
- df_R = r - 1
  - = 2-1
    = 1
  s_R² = SS_R / df_R
  - = 63.0125 / 1
    = 63.0125

In Step 6, we calculate the sum-of-squares for the columns (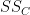 $SS_{C}$ ):

$\sum_{c} (\overline{X}_c - \overline{X})^2$

where c ranges over columns.

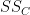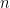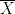$SS_{C}$ = ( $\overline{X}_{4-week}$ - $\overline{X}$ )² + ( $\overline{X}_{12-week}$ - $\overline{X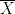}$ )²]
- = 10 [(5.95 - 6.575)² + (7.2 - 6.575)²]
  = 10 [0.390625 + 0.390625]
  = 10 [0.78125]
  = 7.8125
- df_C = c - 1
  - = 2-1
    = 1
  s_C² = SS_C / df_C
  - = 7.8125 / 1
    = 7.8125

In Step 7, calculate the sum-of-squares for the interaction (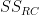 $SS_{RC}$ ):

SS_RC = SS_B - SS_R - SS_C
- = 81.3375 - 63.0125 - 7.8125
  = 10.5125
- df_RC = (r - 1)(c - 1)
  - = (2-1)(2-1)
    = 1
  s_RC² = SS_RC / df_RC
  - = 10.5125 / 1
    = 10.5125

Now, in Step 8, we'll calculate the total sum-of-squares ( $SS_{T}$ ):

SS_T = SS_B + SS_W + SS_R + SS_C + SS_RC
- = 81.3375 + 24.8 + 63.0125 + 7.8125 + 10.5125
  = 187.475
df_T = N - 1
- = 20-1
  = 19

At Step 9, we calculate the F values:

F_R = s_R² / s_W²
- = 63.0125 / 1.55
  = 40.65323
F_C = s_C² / s_W²
- = 7.8125 / 1.55
  = 5.040323
F_RC = s_RC² / s_W²
- = 10.5125 / 1.55
  = 6.782258

And, finally, at Step 10, we can organize all of the above into a table, along with the appropriate F_CRIT values (looked up in a table like this one) that we'll use for comparison and interpretation of our computations:

F_CRIT (1, 16) _α=0.5 = 4.49

ANOVA TABLE
Source	SS	df	s²	F_obt	F_crit	p
rows	63.0125	1	63.0125	40.65323	4.49	p < 0.05
columns	7.8125	1	7.8125	5.040323	4.49	p < 0.05
r * c	10.5125	1	10.5125	6.782258	4.49	p < 0.05
within	24.8	16	1.55	--	--	--
total	187.475	19	--	--	--	--

Both factors (prenatal-exposure and age) are significant, as indicate by the fact that F_OBT > F_CRIT. Thus, we can reject all H₀₁ and H₀₂ and conclude that dendritic spine density is affected by prenatal exposure and age. The interaction between the two factors (r * c) is also significant. Thus, we can also reject H₀₃ and conclude there is a significant interaction between these two factors.

To further interpret these results, we can plot the group means as follows:

Means by group

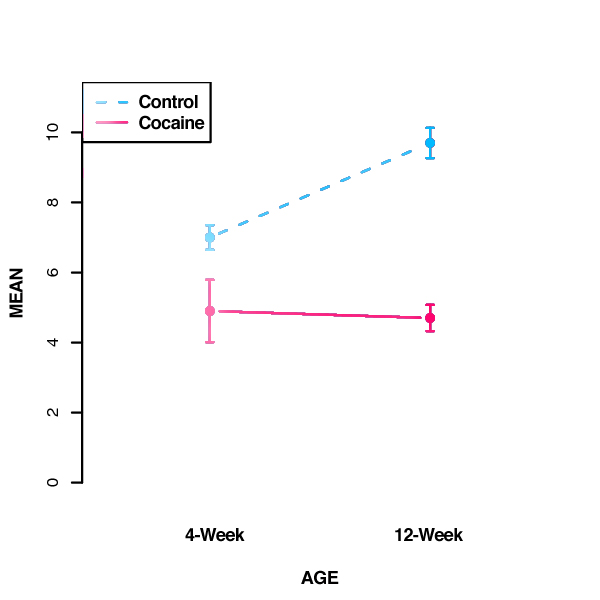
So, as indicated above, spine density is significantly greater in the control group as compared to drug-exposed animals at both 4 and 12 weeks of age. The effect of prenatal drug exposure is magnified with time due to a developmental increase in spine density that occurs only in the control group. Between 4 and 12 weeks of age, spine density in prefrontal cortex increases significantly in control animals, while it remains relatively unchanged in the drug-exposed animals.

IMPORTANT CAVEAT: Please note that the statistics provided by the ANOVA quantify the effect of each factor (prenatal-exposure and age). These statistics do not compare individual condition means, such as whether 4-week control differs from 12-week control. There are 4*3 possible comparisons between these group means, and statistical testing of these individual comparisons requires a post-hoc analysis such as Tukey's HSD (Honestly Significant Difference) Test.

Tukey's HSD (Honestly Significant Difference) Test

Tukey's test is a single-step multiple comparison procedure and statistical test generally used in conjunction with an ANOVA to find which means are significantly different from one another. It compares all possible pairs of group means. Tukey's test is based on a formula very similar to that of the t-test, except that it corrects for experiment-wise error rate. (When there are multiple comparisons being made, the probability of making a type I error increases, so Tukey's test corrects for this.) The formula for a Tukey's test is:

The formula for Tukey's test is:

$q_{obt} = (Y_{A} - Y_{B}) / SE$

where where Y_A is the larger of the two means being compared, Y_B is the smaller, and SE is the standard error of the data in question. Once computed, the q_obt value is compared to a q-value from the q distribution. If the q_obt value is larger than the q_crit value from the distribution, the two means are significantly different.

So, if we wanted to use a Tukey's test to determine whether 4-week control significantly differs from 12-week control, we'd calculate it as follows

q_obt = $\overline{X}_{4-week, control}$ - $\overline{X}_{12-week, control}$ / SE
- = 7 - 9.7 / SE

Multiple Regression

Another analysis technique you could use is a multiple regression. In multiple regression, we find coefficients for each group such that we are able to best predict the group means. The multiple regression computes standard errors on the coefficients, meaning that we can determine if a coefficient is significantly different from zero. On this simple example, multiple regression will give identical answers to ANOVA, but in more complex cases, multiple regression is a more powerful technique that allows you to include additional nuisance predictors, that the analysis controls for before testing for significance of your independent variables.

Go back to the Homepage

-  ⇤ ← Revision 137 as of 2011-11-30 05:20:25 → 
  Size: 13754
  Editor: CelesteKidd
  Comment:
+   ← Revision 138 as of 2011-11-30 05:22:20 → ⇥
  Size: 13752
  Editor: CelesteKidd
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 234:
-q_{OBT} = (Y_{A} - Y_{B}) / SE
\]
}}}

where where ''Y'',,A,, is the larger of the two means being compared, ''Y'',,B,, is the smaller, and SE is the ''standard error'' of the data in question. Once computed, the ''q,,OBT,,'' value is compared to a ''q''-value from the ''q'' distribution. If the ''q,,OBT,,'' value is ''larger'' than the ''q,,CRIT,,'' value from the distribution, the two means are significantly different.
+q_{obt} = (Y_{A} - Y_{B}) / SE
\]
}}}

where where ''Y'',,A,, is the larger of the two means being compared, ''Y'',,B,, is the smaller, and SE is the ''standard error'' of the data in question. Once computed, the ''q,,obt,,'' value is compared to a ''q''-value from the ''q'' distribution. If the ''q,,obt,,'' value is ''larger'' than the ''q,,crit,,'' value from the distribution, the two means are significantly different.
 Line 242:
-''q,,OBT,,'' = <<latex($\overline{X}_{4-week, control}$)>> - <<latex($\overline{X}_{12-week, control}$)>> / SE
''q,,OBT,,'' = 7 - 9.7 / SE
+   ''q,,obt,,'' = <<latex($\overline{X}_{4-week, control}$)>> - <<latex($\overline{X}_{12-week, control}$)>> / SE
        = 7 - 9.7 / SE