Differences between revisions 95 and 104 (spanning 9 versions)

Situations with more than two variables of interest

When considering the relationship among three or more variables, an interaction may arise. Interactions describe a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of Multiple Regression analyses, but they may also be evaluated using Two-Way ANOVA.

Example Problem
Two-Way ANOVA
Multiple Regression

An Example Problem

Suppose we are interested in studying the effects of cocaine on sleep. We might design an experiment to simultaneously test whether both the use of cocaine and the duration of usage affect the number of hours a squirrel will sleep in a night. We might give half of the squirrels we test cocaine, and the other half a placebo substance (the substance variable). And we might vary the duration of usage by administering cocaine or placebo for one of two possible durations before test, 4 weeks or 12 weeks (the duration variable). We can then consider the average treatment response (e.g. number of hours slept) for each squirrel, as a function of the treatment combination that was administered (e.g. substance and duration). The following table shows one possible situation:

HOURS SLEPT IN SINGLE NIGHT
4-Week Placebo (Control)	4-Week Cocaine	12-Week Placebo (Control)	12-Week Cocaine
7.5	5.5	8.0	5.0
8.0	3.5	10.0	4.5
6.0	4.5	13.0	4.0
7.0	6.0	9.0	6.0
6.5	5.0	8.5	4.0

There are three null hypotheses we may want to test. The first two test the effects of each factor under investigation:

H₀₁: Both substance groups sleep for the same number of hours on average.
H₀₂: Both treatment duration groups sleep for the same number of hours on average.

And the third tests for an interaction between these two factors:

H₀₃: The two factors are independent or there is no interaction effect.

Two-Way ANOVA

A two-way ANOVA is an analysis technique that quantifies how much of the variance in a sample can be accounted for by each of two categorical variables and their interactions.

Step 1 is to compute the group means (for each cell, row, and column):

GROUP MEANS
	4-Week	12-Week	All Durations
Placebo	7	9.7	8.35
Cocaine	4.9	4.7	4.8
All Substances	5.95	7.2	6.575

Step 2 is to calculate the sum of squares (SS) for each group (cell) using the following formula:

$\sum_{i=1} (x_{i,g} - \overline{X}_g)^2$

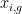where $x_{i,g}$ is the i'th measurement for group g, and $\overline{X}_g$ is the overall group mean for group g.

For each group, this formula is implemented as follows:

4-Week Placebo:
- {7, 8, 6, 7, 6.5}, $\overline{X}_{4-week, placebo}$ = 7
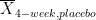  $SS_{4-week, placebo}$ = (7-7)² + (8-7)² + (6-7)² + (7-7)² + (6.5-7)² = 2.25
4-Week Cocaine:
- {5.5, 3.5, 4.5, 6, 5}, $\overline{X}_{4-week, cocaine}$ = 4.9
  $SS_{4-week, cocaine}$ = (5.5-4.9)² + (3.5-4.9)² + (4.5-4.9)² + (6-4.9)² + (5-4.9)² = 3.7
12-Week Placebo:
- {8, 10, 13, 9, 8.5}, $\overline{X}_{12-week, placebo}$ = 9.7
  $SS_{12-week, placebo}$ = (8-9.7)² + (10-9.7)² + (13-9.7)² + (9-9.7)² + (8.5-9.7)² = 15.8
12-Week Cocaine:
- {5, 4.5, 4, 6, 4}, $\overline{X}_{12-week, cocaine}$ = 4.7
  $SS_{12-week, cocaine}$ = (5-4.7)² + (4.5-4.7)² + (4-4.7)² + (6-4.7)² + (4-4.7)² = 2.8

Step 3 is to calculate the between-groups sum of squares(SS_B):

$n \cdot \sum_{g} (\overline{X}_g - \overline{X})^2$

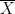where n is the number of subjects in each group, $\overline{X}_g$ is the mean for group g, and $\overline{X}$ is the overall mean (across groups).

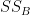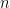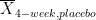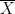$SS_{B}$ = [( $\overline{X}_{4-week, placebo}$ - $\overline{X}$ )² + ( $\overline{X}_{4-week, cocaine}$ - $\overline{X}$ )² + ( $\overline{X}_{12-week, placebo}$ - $\overline{X}$ )² + ( $\overline{X}_{12-week, cocaine}$ - $\overline{X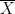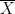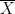}$ )²]
- = 5 [(7 - 6.575 )² + (4.9 - 6.575)² + (9.7 - 6.575)² + (4.7 - 6.575)²]
  = 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]
  = 5 [16.2675]
  = 81.3375

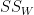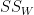Now, Step 4 , we'll calculate the sum-of-squares within groups ( $SS_{W}$ ):

$SS_{W}$ = $SS_{4-week, placebo}$ + $SS_{4-week, cocaine}$ + $SS_{12-week, placebo}$ + $SS_{12-week, cocaine}$
- = 2.25 + 3.7 + 15.8 + 2.8
  = 24.55
$df_{w}$ =
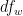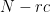
- = 20 - (2 * 2)
  = 16
$s_{W}$ ² = $SS_{W}$ / $df_{w}$
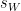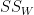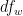
- = 24.55 / 16
  = 1.534375

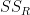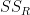For Step 5, we'll calculate the sum-of-squares for the rows( $SS_{R}$ ):

$SS_{R}$ =

latex error! exitcode was 1 (signal 0), transscript follows:

This is pdfTeX, Version 3.14159265-2.6-1.40.19 (TeX Live 2019/dev/Debian) (preloaded format=latex)
entering extended mode
(./latex_17e6d98cfcfc32261c2f3dbba9b765ae7942e8ed_p.tex
LaTeX2e <2018-12-01>
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2018/09/03 v1.4i Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo))
(/usr/share/texlive/texmf-dist/tex/latex/base/inputenc.sty)
No file latex_17e6d98cfcfc32261c2f3dbba9b765ae7942e8ed_p.aux.
! Undefined control sequence.
<recently read> \n 
                   
l.7 $\n
       $
[1] (./latex_17e6d98cfcfc32261c2f3dbba9b765ae7942e8ed_p.aux) )
(see the transcript file for additional information)
Output written on latex_17e6d98cfcfc32261c2f3dbba9b765ae7942e8ed_p.dvi (1 page,
 152 bytes).
Transcript written on latex_17e6d98cfcfc32261c2f3dbba9b765ae7942e8ed_p.log.

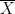[( $\overline{X}_{placebo}$ - $\overline{X}$ )² + ( $\overline{X}_{cocaine}$ - $\overline{X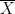}$ )²]

= 10 [(8.35 - 6.575)² + (4.8 - 6.575)²]
= 10 [3.150625 + 3.150625]
= 10 [6.30125]
= 63.0125

df_R = r - 1
- = 2-1
  = 1
s_R² = SS_R / df_R
- = 63.0125 / 1
  = 63.0125

In Step 6, we calculate the SS_C:

SS_C = n [( M_4-Week - M_Group )² + ( M_12-Week - M_Group)²]
- = 10 [(5.95 - 6.575)² + (7.2 - 6.575)²]
  = 10 [0.390625 + 0.390625]
  = 10 [0.78125]
  = 7.8125
- df_C = c - 1
  - = 2-1
    = 1
  s_C² = SS_C / df_C
  - = 7.8125 / 1
    = 7.8125

In Step 7, calculate the SS_RC:

SS_RC = SS_B - SS_R - SS_C
- = 81.3375 - 63.0125 - 7.8125
  = 10.5125
- df_RC = (r - 1)(c - 1)
  - = (2-1)(2-1)
    = 1
  s_RC² = SS_RC / df_RC
  - = 10.5125 / 1
    = 10.5125

Now, in Step 8, we'll calculate the SS_T:

SS_T = SS_B + SS_W + SS_R + SS_C + SS_RC
- = 81.3375+ 24.55 + 63.0125 + 7.8125 + 10.5125
  = 187.225
df_T = N - 1
- = 20-1
  = 19

At Step 9, we calculate the F values:

F_R = s_R² / s_W²
- = 63.0125 / 1.534375
  = 41.06721
F_C = s_C² / s_W²
- = 7.8125 / 1.534375
  = 5.09165
F_RC = s_RC² / s_W²
- = 10.5125 / 1.534375
  = 6.851324

And, finally, at Step 10, we can organize all of the above into a table, along with the appropriate F_CRIT values (looked up in a table like this one) that we'll use for comparison and interpretation of our computations:

F_CRIT (1, 16) _α=0.5 = 4.49

ANOVA TABLE
Source	SS	df	s²	F_obt	F_crit	p
rows	63.0125	1	63.0125	41.06721	4.49	p < 0.05
columns	7.8125	1	7.8125	5.09165	4.49	p < 0.05
r * c	10.5125	1	10.5125	6.851324	4.49	p < 0.05
within	24.55	16	1.534375	--	--	--
total	187.225	19	--	--	--	--

[INTERPRETATION HERE]

Multiple Regression

[BASIC INFO ABOUT MULTIPLE REGRESSION]

-  ⇤ ← Revision 95 as of 2011-11-25 17:03:22 → 
  Size: 8352
  Editor: CelesteKidd
  Comment:
+   ← Revision 104 as of 2011-11-25 17:28:37 → ⇥
  Size: 8862
  Editor: CelesteKidd
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 53:
-  <<latex($\overline{X}_{4-week, placebo}$)>> = 7, {7, 8, 6, 7, 6.5}<<BR>>
  '''''SS,,4-Wk Placebo,,''''' = (7-7)^2^ + (8-7)^2^ + (6-7)^2^ + (7-7)^2^ + (6.5-7)^2^ = '''2.25'''<<BR>><<BR>>
+-Week Placebo: <<BR>>
     {7, 8, 6, 7, 6.5}, <<latex($\overline{X}_{4-week, placebo}$)>> = 7<<BR>>
     <<latex($SS_{4-week, placebo}$)>> = (7-7)^2^ + (8-7)^2^ + (6-7)^2^ + (7-7)^2^ + (6.5-7)^2^ = '''2.25'''<<BR>><<BR>>
-Line 56:
+Line 57:
-  <<latex($\overline{X}_{4-week, cocaine}$)>> = 4.9, {5.5, 3.5, 4.5, 6, 5}<<BR>>
  '''''SS,,4-Wk Cocaine,,''''' = (5.5-4.9)^2^ + (3.5-4.9)^2^ + (4.5-4.9)^2^ + (6-4.9)^2^ + (5-4.9)^2^ = '''3.7'''<<BR>><<BR>>
+-Week Cocaine: <<BR>>
     {5.5, 3.5, 4.5, 6, 5}, <<latex($\overline{X}_{4-week, cocaine}$)>> = 4.9<<BR>>
     <<latex($SS_{4-week, cocaine}$)>> = (5.5-4.9)^2^ + (3.5-4.9)^2^ + (4.5-4.9)^2^ + (6-4.9)^2^ + (5-4.9)^2^ = '''3.7'''<<BR>><<BR>>
-Line 59:
+Line 61:
-  <<latex($\overline{X}_{12-week, placebo}$)>> = 9.7, {8, 10, 13, 9, 8.5}<<BR>>
  '''''SS,,12-Wk Placebo,,''''' = (8-9.7)^2^ + (10-9.7)^2^ + (13-9.7)^2^ + (9-9.7)^2^ + (8.5-9.7)^2^ = '''15.8'''<<BR>><<BR>>
+-Week Placebo: <<BR>>
     {8, 10, 13, 9, 8.5}, <<latex($\overline{X}_{12-week, placebo}$)>> = 9.7<<BR>>
     <<latex($SS_{12-week, placebo}$)>> = (8-9.7)^2^ + (10-9.7)^2^ + (13-9.7)^2^ + (9-9.7)^2^ + (8.5-9.7)^2^ = '''15.8'''<<BR>><<BR>>
-Line 62:
+Line 65:
-  <<latex($\overline{X}_{12-week, cocaine}$)>> = 4.7, {5, 4.5, 4, 6, 4}<<BR>>
  '''''SS,,12-Wk Cocaine,,''''' = (5-4.7)^2^ + (4.5-4.7)^2^ + (4-4.7)^2^ + (6-4.7)^2^ + (4-4.7)^2^ = '''2.8'''<<BR>><<BR>>
+-Week Cocaine: <<BR>>
     {5, 4.5, 4, 6, 4}, <<latex($\overline{X}_{12-week, cocaine}$)>> = 4.7<<BR>>
     <<latex($SS_{12-week, cocaine}$)>> = (5-4.7)^2^ + (4.5-4.7)^2^ + (4-4.7)^2^ + (6-4.7)^2^ + (4-4.7)^2^ = '''2.8'''<<BR>><<BR>>
-Line 77:
+Line 81:
-  '''''SS,,B,,''''' =  ''n'' [( ''M,,4-Wk Placebo,,'' - ''M,,Group,,'' )^2^ + ( ''M,,4-Wk Cocaine,,'' - ''M,,Group,,'')^2^ + ( ''M,,12-Wk Placebo,,'' - ''M,,Group,,'' )^2^ + ( ''M,,12-Wk Cocaine,,'' - ''M,,Group,,'')^2^]<<BR>>
      = 5 [(7 - 6.575 )^2^ + (4.9 - 6.575)^2^ + (9.7 - 6.575)^2^ + (4.7 - 6.575)^2^]<<BR>>
      = 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]<<BR>>
      = 5 [16.2675]<<BR>>
      = '''81.3375'''<<BR>><<BR>>
+  <<latex($SS_{B}$)>> =  <<latex($n$)>> [( <<latex($\overline{X}_{4-week, placebo}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{4-week, cocaine}$)>> - <<latex($\overline{X}$)>>)^2^ + ( <<latex($\overline{X}_{12-week, placebo}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{12-week, cocaine}$)>> - <<latex($\overline{X}$)>>)^2^]<<BR>>
     = 5 [(7 - 6.575 )^2^ + (4.9 - 6.575)^2^ + (9.7 - 6.575)^2^ + (4.7 - 6.575)^2^]<<BR>>
     = 5 [0.180625 + 2.805625 + 9.765625 + 3.515625]<<BR>>
     = 5 [16.2675]<<BR>>
     = '''81.3375'''<<BR>><<BR>>
-Line 83:
+Line 87:
-Now, '''Step 4''' , we'll calculate the ''SS,,W,,'':<<BR>>
   '''''SS,,W,,''''' = ''SS,,4-Wk Placebo,,'' + ''SS,,4-Wk Cocaine,,'' + ''SS,,12-Wk Placebo,,'' + ''SS,,12-Wk Cocaine,,''<<BR>>
+Now, '''Step 4''' , we'll calculate the sum-of-squares within groups (<<latex($SS_{W}$)>>):<<BR>>
   <<latex($SS_{W}$)>> = <<latex($SS_{4-week, placebo}$)>> + <<latex($SS_{4-week, cocaine}$)>> + <<latex($SS_{12-week, placebo}$)>> + <<latex($SS_{12-week, cocaine}$)>><<BR>>
-Line 88:
+Line 92:
-   '''''df,,W,,''''' = ''N - rc ''<<BR>>
+   <<latex($df_{w}$)>> = <<latex($N - rc$)>><<BR>>
-Line 92:
+Line 96:
-   '''''s,,W,,^2^''''' = ''SS,,W,,'' /  ''df,,W,,''<<BR>>
+   <<latex($s_{W}$)>>^2^ = <<latex($SS_{W}$)>> /  <<latex($df_{w}$)>><<BR>>
-Line 96:
+Line 100:
-For '''Step 5''', we'll calculate the ''SS,,R,,'':<<BR>>
+For '''Step 5''', we'll calculate the sum-of-squares for the rows(<<latex($SS_{R}$)>>):<<BR>>
-Line 98:
+Line 102:
-  '''''SS,,R,,''''' =  ''n'' [( ''M,,Placebo,,'' - ''M,,Group,,'' )^2^ + ( ''M,, Cocaine,,'' - ''M,,Group,,'')^2^]<<BR>>
+  <<latex($SS_{R}$)>> =  <<latex($\n$)>> [( <<latex($\overline{X}_{placebo}$)>> - <<latex($\overline{X}$)>> )^2^ + ( <<latex($\overline{X}_{cocaine}$)>> - <<latex($\overline{X}$)>>)^2^]<<BR>>