One-Way ANOVA

In the last section we discussed the independent groups t-test and the paired groups t-test. Those tests are generally applicable to experimental designs with two groups of data. In this section, we are going to review the one-way ANOVA test, which is useful in experimental designs with three or more groups. Similarly, there is independent groups one-way ANOVA and repeated measures (correlated samples) one-way ANOVA. The reasoning behind the distinction is the same as in the t-test.

Our primary interest here is to determine if there are significant differences between these groups with respect to one particular variable.

An Example Problem

In class, we collected data on students' TV watching habits (# hours watched per week) and their majors. Below is tabulated a subset of the data on # of TV hours watched grouped by student major. All but five students in the class were NSC or BCS majors, so we randomly selected 5 NSC majors, 5 BCS majors and all 5 "other" majors to use as sample data for this problem. The data (# of TV hours watched) grouped by major for these 15 students is listed below.

NSC	BCS	Other
12	0	4
15	5	10
1	15	6
10	15	0
10	10	7

The null hypothesis for a one-way ANOVA test is that the population means of the groups are equal. In mathematical terms, the null hypothesis states 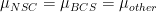$\mu_{NSC} = \mu_{BCS} = \mu_{other}$ , where each 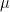$\mu$ stands for the population mean (in terms of hours of TV watched) of each corresponding group. The one-way ANOVA test is conducted to test whether we should accept or reject this null hypothesis.

The idea behind the ANOVA test is in fact quite simple: if the variance between the groups is significantly larger than the variance within groups, there is probably a true difference between the population means of these groups. In other words, we examine how groups differ between each other while taking into consideration how variable each group of data are individually. Below we show the steps of implementing the ANOVA test.

Within-group variance estimate

To calculate the within-group variance estimate, we first calculate the mean number of hours of TV watched for each group. This can be obtained by simply averaging the numbers along columns in the above table. Therefore, we get:

$\overline{x}_{NSC}=9.6$ , $\overline{x}_{BCS}=9$ , $\overline{x}_{other}=5.4$

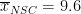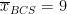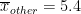
As an intermediate step, the within-groups sum-of-squares (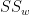 $SS_{w}$ ) are calculated. 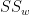$SS_{w}$ can be intuitively viewed as a measure that summarizes the difference between individual data points and the mean. So, for the neuroscience majors:

$SS_{NSC} = \sum_{i} (x_{NSC_{i}} - 9.6)^{2} = (12-9.6)^2 + (15-9.6)^2 + (1-9.6)^2 + (10-9.6)^2 + (10-9.6)^2 = 109.20$

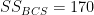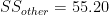Similarly, it is not difficult to get $SS_{BCS}=170$ and $SS_{other}=55.20$ . The within-groups sum-of-squares is the sum of all group sum-of-squares: $SS_{w} = SS_{NSC} + SS_{BCS} + SS{other} = 334.4$ .

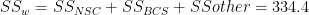So far, we have got the 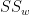$SS_{w}$ , but it is not the within-groups variance estimate -- 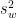$s^{2}_{w}$ yet. What is a reasonable way of deriving the estimate? Note that if we collect a relatively large data set for each of the groups, chances are the within-groups sum-of-squares is going to be relatively large (why? try to understand the intuition). Therefore, to derive the within-groups variance estimate, we need to identify the degrees of freedom for 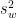$s^{2}_{w}$ . The DF for 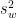$s^{2}_{w}$ is the number of total data points minus the number of groups. That is: $df_{w} = N - k = 15 -3 = 12$ .

Thus, finally, the within-groups variance estimate is

$s^{2}_{w} = \frac{SS_{w}}{df_{w}} = \frac{334.4}{12} = 27.87$

Between-groups variance estimate

Similarly, we must calculate the between-groups sum-of-squares in order to get the between-groups variance estimate. The first step is to get the overall mean of all collected samples across groups.

$\bar{x}_{overall} = 8$

The between-groups sum-of-squares is calculated as in the following formula, where n is the size of individual groups. Intuitively, this captures how variable one group is from another.

$SS_{B} = n\sum_{x \in NSC,BCS,other} (x - \bar{x}_{overall})^{2} = 5((9.6-8)^2 + (9-8)^2 + (5.4-8)^2) = 51.6$

The degrees of freedom for the between-groups variance estimate is simply the number of groups minus one: 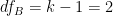$df_{B} = k -1 = 2$ . Therefore, the between-groups variance estimate is

$s^{2}_{B} = \frac{SS_{B}}{df_{B}} = \frac{51.6}{2} = 25.8$

F Statistic

The last step in conducting an ANOVA test is calculating the F statistic. This is actually an easy step of dividing the between-groups variance estimate 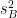$s^{2}_{B}$ by the within-groups variance estimate 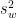$s^{2}_{w}$ . For the current problem, this gives us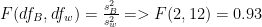 $F(df_{B}, df_{w}) = \frac{s^{2}_{B}}{s^{2}_{w}} => F(2,12) = 0.93$

Lastly, use the table of critical values of F in the back of your textbook to find the critical value of F for a .05 significance level. We found the critical value is 3.88 given the two degrees of freedom values. Clearly, our obtained F value is smaller than the critical value, and we fail to reject the null hypothesis: there is not sufficient evidence that NSC, BCS and other majors watch different amounts of TV.

Post-hoc Tukey HSD Test

In the above example, the main effect came out non-significant. Had it been significant, we would want to know which groups are different from one other. In fact, even if the F-test is not significant, there could be a significant difference between 2 of the groups (particularly if the F value approaches significance). This is where the investigator needs to look at the data, and use common sense to decide whether a further probe into the data is appropriate. There are three possible situations: NSC and BCS students are different, BCS and "other" students are different, or NSC and "other" students are different. Any combination of these three situations may contribute to the main effect of one-way ANOVA, and any one could exist in the absence of a main effect.

When it is necessary to test which two groups are different from each other, a common tool is the Tukey test. The Tukey test is a post-hoc test in the sense that the pairwise comparison tests are conducted after the ANOVA test. Importantly, it keeps the familywise error rate at 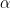$\alpha$ =.05 (rather than setting the per comparison error rate at 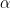$\alpha$ =.05, as is the case with a t-test). So if 3 posthoc comparisons are made, the probability that we will make at least one Type I error is held at 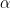$\alpha$ =.05. We will only provide the formula of the Tukey test here.

In order to know whether a pair of groups (for example, the NSC and the BCS, had the one-way ANOVA obtained a significant result) differ from each other, we calculate the Q statistic:

$Q_{obt} = \frac{|\bar{x}_{NSC} - \bar{x}_{BCS}|}{\sqrt{s^{2}_{w}/n}}$

That is, the Q statistic is the absolute difference between the group means, divided by the square root of within-groups variance estimate divided by the number of subjects in each group. After calculating the Q statistic, we can look up in the Q distribution table for the Q critical value. The degrees of freedom is the same as the DF for 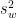$s^{2}_{w}$ , which we have calculated above.

We recommend using the Vassar statistics tools for conducting the Tukey test (along with many other statistics tests reviewed in this Wiki). The direct link for the ANOVA test is:

http://faculty.vassar.edu/lowry/anova1u.html

Please try it yourself. Be sure to select "Independent Samples" and "weighted" for the main ANOVA test. Change the original data so that the ANOVA yields a significant result and then review the Tukey results at the bottom of that page.

Repeated-measures ANOVA

For the difference between independent groups and repeated measures design, please read the section on t-tests. It is important to understand that repeated measures mean the measurements are taken from the same pool of subjects under different conditions. We will not go over the formulas as they get fairly complex. However, we do recommend using the Vassar stats to conduct a repeated measures ANOVA with the same data as in the above example. In that case, we can imagine those data points are collected from 5 students who have changed their majors three times.

The direct link for the ANOVA test is:

http://faculty.vassar.edu/lowry/anova1u.html

Notice the different test results. Why is that the case? Can you come up with an intuitive explanation for that? What does this tell us about choosing the right experimental design?

Go back to the Homepage