Statistical Tests for Experiments with Three or More Samples

In the last section we discussed the independent groups t-test and the correlated groups t-test. Those tests are generally applicable to experimental designs with two groups of data. In this section, we are going to review the one-way ANOVA test, which is useful in experimental designs with three or more groups. Our primary interest here is to determine if there are significant differences between these groups with respect to one particular variable.

An Example of One-way ANOVA

An Example Problem

In class, we collected data on students' TV watching habits (# hours watched per week) and their majors. Below is tabulated a subset of the data on # of TV hours watched grouped by student major. All but five students in the class were NSC or BCS majors, so we randomly selected 5 NSC majors, 5 BCS majors and all 5 "other" majors to use as sample data for this problem. The data (# of TV hours watched) grouped by major for these 15 students is listed below.

NSC	BCS	Other
12	0	4
15	5	10
1	15	6
10	15	0
10	10	7

The null hypothesis for a one-way ANOVA test is that groups means are equal. In mathematical terms, the null hypothesis states 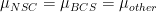$\mu_{NSC} = \mu_{BCS} = \mu_{other}$ , where each 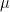$\mu$ stands for the population mean (in terms of hours of TV watched) of each corresponding group. The one-way ANOVA test is conducted to test whether we should accept or reject this null hypothesis.

The idea behind the ANOVA test is in fact quite simple: if the variance between the groups is significantly larger than the variance within groups, there is probably a true difference between the population means of these groups. In other words, we examine how groups differ between each other while taking into consideration how variable each group of data are individually. Below we should the steps of implementing the ANOVA test.

Within-group variance estimate

To calculate the within-group variance estimate, we first calculate the mean number of hours of TV watched for each group. This can be obtained by simply averaging the numbers along columns in the above table. Therefore, we get:

$\overline{x}_{NSC}=9.6$ , $\overline{x}_{BCS}=9$ , $\overline{x}_{other}=5.4$

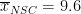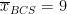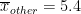
As an intermediate step, the within-groups sum-of-squares (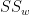 $SS_{w}$ ) are calculated. 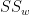$SS_{w}$ can be intuitively viewed as a measure that summarizes the difference between individual data points and the mean. So, for the neuroscience majors:

$SS_{NSC} = \sum_{i} (x_{NSC_{i}} - 9.6)^{2} = (12-9.6)^2 + (15-9.6)^2 + (1-9.6)^2 + (10-9.6)^2 + (10-9.6)^2 = 109.20$

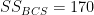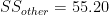Similarly, it is not difficult to get $SS_{BCS}=170$ and $SS_{other}=55.20$ . The within-groups sum-of-squares is the sum of all group sum-of-squares: $SS_{w} = SS_{NSC} + SS_{BCS} + SS{other} = 334.4$ .

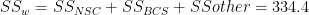So far, we have got the 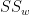$SS_{w}$ , but it is not the within-groups variance estimate yet. What is a reasonable way of deriving the estimate? Note we haven't paid any attention to the size of our sample data yet. If we collected a relatively large sample data, chances are the